Модифицированная программа

Cтраница 1

Модифицированная программа 26 страдает незначительным дефектом стиля, заключающимся в помещении символа Л внутрь множества процедур печать, поскольку эти процедуры теперь уже нельзя вызывать, не порождая при этом новые факты, что приводит к некоторой потере их гибкости. Более изящный подход, дающий более модульную структуру, состоит в использовании нового множества процедур, цель которого - только образовывать множество фактов, не делая никаких предположений относительно их дальнейшего употребления. [1]

Листинг модифицированной программы приведен в конце этого параграфа. [2]

Приведем модифицированную программу для обработки арифметических выражений, в которой используется стандартный механизм возврата ненужных динамических переменных. [3]

В модифицированной программе для далеких от ребра граней проводятся только тривиальные вычисления прямоугольника грани и сравнение этого прямоугольника с прямоугольником ребра. Поскольку для каждого конкретного ребра подавляющая масса граней являются далекими, то скорость построения изображения полиэдра возрастет примерно во столько раз, во сколько фильтрование быстрее учета тени от грани на ребро. Таким образом, фильтр тем лучше, чем меньше граней он пропускает и чем быстрее он работает. Эти требования являются противоречивыми. Идеальным по критерию минимума граней является фильтр, который пропускает только действительно затеняющие ребро грани. Однако определение таких граней почти не отличается от нахождения тени от грани на ребро и никакого выигрыша в скорости не дает. Идеальным по критерию скорости работы является фильтр, который пропускает все грани вообще, но применение такого фильтра бессмысленно. [4]

Для испытания модифицированной программы была проведена новая серия экспериментов. Чтобы уменьшить время обучения, первоначальный выбор членов оценочного полинома был сделан на основе предыдущих экспериментов, но их веса были выбраны произвольно. Исправленная программа в противоположность беспорядочному поведению в первой серии экспериментов оказалась очень стабильной, возможно, за счет несколько более низкой начальной скорости обучения. [5]

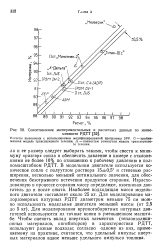Сопоставление экспериментальных и расчетных данных по экономичности РДТТ. [6]

Расчеты выполнены с использованием модифицированной программы SPP. [7]

Программа КРА-КИН представляет собой модифицированную программу СИСТ-РКН. Изменена лишь основная программа и в подпрограмме 10000 записаны соответствующие дифференциальные уравнения. [8]

Список дополнительных идентификаторов программы ЭФФСТИСП. [9]

В данной главе будет описана модифицированная программа ЭФФСТИСП, которая ищет оптимальное парораспределение, при котором концентрация отдельной примеси в паре или его общее солесодержание будет минимальным. [10]

На рис. 4.11 изображены текст модифицированной программы определения времени года по номеру месяца и два возможных результата ее работы: для неправильного ввода данных и для правильного ввода. [11]

Работа оператора OVERLAY. [12]

Если оператор OVERLAY содержал необязательную часть с указанием номера строки, то управление передается на эту строку в модифицированной программе по правилам обращения к подпрограмме. В ином случае управление передается оператору, следующему за оператором OVERLAY. [13]

Как можно видеть из рис. 2.22 различия в расчетах коэффициентов отклонения при гипотезе В, проведенных Стори и Хаммером ( 1995) и по модифицированной программе Салема и Броклехурста ( 1979), существенны для малых квантовых уров ней. Хотя Салем и Броклехурст ограничили свои опубликован ные таблицы коэффициентов отклонения значениями n 50, Уолмсли ( 1990) продлил их расчеты до n 20, включив для этих низких уровней соударения и ударную ионизацию. [14]

Системы уравнений такого вида не имеют единственного решения. Используя модифицированную программу Г - Ж, приведите соответствующую этой системе матрицу к диагональному виду как можно более точно. Таким образом находят значение переменной X ( S9), которой после исключения недиагональных элементов по обычному методу Гаусса - Жордана можно присвоить любое значение. В 59 - м столбце на диагонали и под ней могут находиться только нули. Если дополнить 89 - й столбец в 89 - й строке элементом, равным - 1, то элементы этого столбца станут компонентами искомого собственного вектора. Этот собственный вектор обычно нормируют на единичную длину. Для этого находят длину вектора ( квадратный корень из суммы квадратов компонентов) и каждый компонент вектора делят на эту длину. [15]

Страницы: 1 2