Прогрессия

Cтраница 1

Прогрессии, как мы уже знаем, были известны еще в глубокой древности. [1]

Прогрессии - это последовательности чисел, построенные по определенным правилам. Прогрессии бывают арифметическими и геометрическими. [2]

Прогрессия завершается, когда структура в заголовке утверждения специфицируется константным термом. Обычно таким утверждением является факт. [3]

Прогрессии определяются двумя элементами: первым членом и разностью в случае арифметической и первым членом и знаменателем в случае геометрической прогрессии. Если прогрессии конечны, то для их определения нужно знать и п - число членов. [4]

Прогрессии а1 ( а2, а3 и аа, а2, at считаются различными. [5]

Прогрессии полос, наблюдаемые в спектрах SiH2 и РН2, очень похожи на красные полосы СН2 и а-полосы NH2 ( Герцберг и Верма [526], Рамсей [1042]), хотя системы полос SiH2 и РН2 имеют значительно более сложную структуру, чем соответствующие полосы СН2 и NH2 - Анализ одной из полос РН2 недавно был завершен Диксоном, Даксбери и Рамсеем [2866], но в то же время ни одна из полос 8Ш2 до сих пор не проанализирована. Колебательные интервалы в возбужденных состояниях РН2 и SiH2 сначала закономерно уменьшаются, а затем заметно возрастают, а это, как впервые отметил Диксон [285], указывает на существенное отклонение от линейной структуры в возбужденном состоянии ( фиг. [6]

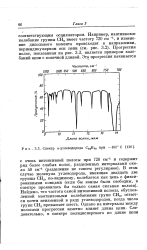Спектр - углеводорода С24Н60 при - 160 С. [7]

Прогрессия полос, показанная на рис. 3.3, является примером колебаний цепи с конечной длиной. [8]

Пример геометрической прогрессии баэ. [9]

Арифметаческая прогрессия баэ малоприменима в инхенерной практике. Зодее подходящей является геометрическая прогрессия. [10]

Прогрессиями здесь называются строки последнего выражения § 323; до бесконечности продолжается последовательность этих строк. [11]

Эти прогрессии, вероятно, представляют собой члены ридберговскоп серии, предел которой связан с четкой границей поглощения при 16 5 эв. Подобная интерпретация подтверждается экспериментами по электронному удару, выполненными Фро-стом и Мак-Дауэлом [401] ( а также более ранней работой Прайса и Сагдена [1023]), которые наблюдали три потенциала появления Н20 при 12 60, 14 35 и 16 34 эв, причем последний, вероятно, соответствует пределу поглощения, найденному Хеннингом. Три потенциала появления должны соответствовать трем электронным состояниям нона Н20 - основному 2Д4 - состоянию, первому возбужденному состоянию типа 2А t при 1 75 эв и второму возбужденному состоянию 2В2 при 3 7 эв ( см. стр. Соответствующие цифры для НзЗ равны 2 0j и 3 78 эв. [12]

Эта прогрессия, возможно, является частью системы В - X. Начиная с 1650 А расположена интенсивная система довольно четких полос, простирающаяся вплоть до 1350 А. Наблюдаемое чередование интенсивности в полосах прогрессии v2 свидетельствует о том, что молекула N02 в верхнем состоянии имеет линейную структуру ( см. стр. Поскольку ион NOf должен иметь структуру, подобную С02, молекула NO2 в ридберговских состояниях должна быть линейной. [13]

Такая прогрессия с Дг - деформ - 1 может наблюдаться только в том случае, если молекула изогнута в возбужденном состоянии ( см. стр. Внутренние соотношения между другими прогрессиями не ясны. [14]

Поскольку прогрессия возрастающая, то значение QI является посторонним. Решив теперь уравнение 2 1 32 2, получим ответ. А Пусть 1 ] г, v2, v3 ( м / мин) - соответственно скорости первого, второго и третьего конькобежцев. [15]

Страницы: 1 2 3 4