Продолжительность - действие - нагрузка
Cтраница 3
Динамический предел текучести Давно было известно, что прочность многих твердых тел заметно увеличивается, когда уменьшается продолжительность действия нагрузки. Однако степень упрочнения в общем случае зависит не только от скорости деформации, но и от механических свойств и структуры материала в исходном ( не нагруженном) состоянии. [31]
При стеклообразном состоянии полимера нагрузка вызывает незначительную упругую деформацию, и ее величина практически не зависит от продолжительности действия нагрузки; после снятия нагрузки тело сразу же восстанавливает первоначальную форму. Время релаксации мало, а энергия теплового движения в данном температурном интервале еще недостаточна для свободного перемещения сегментов. [32]
Рассмотрим другой случай, когда напряжение и деформацию нельзя считать независимыми от времени, когда нужно учитывать и продолжительность действия нагрузки. При расчете напряженного и деформированного состояния в зависимости от времени действия нагрузки, как уже отмечалось, приемлемы методы теории вязко-упругости. При этом наряду с проявлением ползучести происходит значительное падение прочности в зависимости от возрастающей продолжительности действия нагрузки. Таким образом, необходимо рассчитывать размеры несущих элементов конструкций с учетом времени прочности материала. [33]
 |
Твердомер конусный для испытания твердости шлифовальных кругов на вулканито. [34] |
Нагрузка на конус создается в два приема: предварительная - 10 кГ и окончательная - 60 кГ с продолжительностью действия окончательной нагрузки 4 - 5 сек. Показателем твердости является глубина вдавливания конуса. В зависимости от формы и размеров абразивного инструмента испытание производится в трех или четырех точках. [35]
Законы развития трещины, установленные механикой разрушения, показывают, что разрушение металлов является кинетическим процессом, зависящим от продолжительности действия нагрузки, размеров дефекта, свойств стали и рабочих параметров газонефтепроводов. [36]
Полимеры по сравнению с другими материалами, например металлами, отличаются резко выраженной зависимостью механических свойств от температуры и продолжительности действия нагрузки. [37]
Проводимые таким образом прочностные расчеты не соответствуют современным научным представлениям о прочности материалов, поскольку в них не учитывается продолжительность действия нагрузки. Согласно современным представлениям, при очень длительном действии нагрузки любые по величине напряжения приводят к разрушению. Однако для большинства металлов это не имеет практического значения из-за чрезвычайно быстрого возрастания времени до разрушения при незначительном уменьшении напряжения ниже предела прочности. [38]
Все температурные границы смещаются к высоким температурам с увеличением скорости деформации ( в особенности при ударе) и уменьшением продолжительности действия нагрузки. [40]
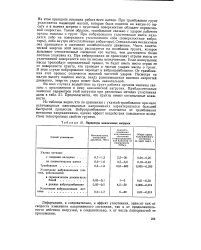 |
Параметры циклических нагрузок. [41] |
Деформация, а следовательно, и эффект уплотнения, зависит как от скорости изменения напряженного состояния, так и от продолжительности действия нагрузки, а следовательно, и от числа повторностей ее приложения. [42]
 |
Кривые ползучести ( а и обобщенная кривая ползучести ( б стеклотекстолита, КАСТ-В при сжатии по утку ткани. напряжения равны. [43] |
Конечной целью эксперимента по определению ползучести является установление функциональной связи между напряжением, деформацией, их производными по времени и продолжительностью действия нагрузки. В теории упругости используются только простейшие функциональные связи между напряжениями, деформациями и их производными без учета влияния продолжительности силового воздействия. Так, закон Гука устанавливает линейную связь между напряжениями и деформациями до уровня напряжений, равных пределу пропорциональности, и одновременно является законом подобия, предусматривающим возможность экстраполяции с одного уровня напряжений и деформаций на другие. Необходимо также найти единую форму функции для изображения семейства кривых ползучести, чтобы кривые ползучести при разных значениях постоянных напряжений были подобными. [44]
Интегральное уравнение (3.5) позволяет разыскать интенсивность контактного давления р ( х, t) в зависимости от положения точки по ширине контакта и продолжительности действия нагрузки. [45]
Страницы: 1 2 3 4
