Производная - скорость
Cтраница 1
Производная скорости по времени называется ускорением материальной точки. [1]
Так как ускорение - это производная скорости по времени, то для того, чтобы найти его значение, нужно продифференцировать эту формулу. Вспомним теперь одно из правил табл. 8.3, а именно что производная суммы равна сумме производных. [2]
Ди / Дг / - средняя производная скорости по направлению, нормальному к направлению потока), влияет на величину измеренной скорости и на ее направление. [3]
Это означает, что в общем случае производная скорости разрыва по длине дуги ударной адиабаты в точке Жуге равна нулю. [4]
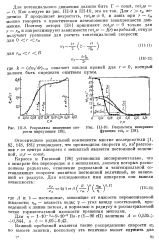 |
Результаты измерения скорости циркуляции f38 ].| Результаты измерения функции rot2 w. [5] |
Относительно радиальной компоненты многие исследователи [1, 82, 148, 181] утверждают, что производная скорости wr на. [6]
Производная силы тока по времени есть не что иное, как вторая производная заряда по времени, подобно тому как производная скорости ( ускорение) есть вторая производная координаты по времени. [7]
Теперь предположим, что в резонансной точке, где фазовая скорость колебаний uo / k AVr0 / ( xc) / 2A; совпадает со скоростью течения VQ ( XS) вторая производная скорости имеет малое, но отличное от нуля значение. Как следует из (10.13) - (10.15), колебания будут нарастать, если величины АУ ( хс) и VQ ( XS) имеют разные знаки. Поскольку скачок первой производной соответствует предельной локализации второй, то условие неустойчивости совпадает с необходимым условием неустойчивости Рэлея. Инкремент неустойчивости может быть получен как с помощью (10.15), так и с использованием уравнения Рэлея. В последнем случае вклад резонансной точки следует учесть по методу последовательных приближений. [8]
Описанное распространение метода Польгаузена на случай отсасывания имеет тот же недостаток, что и метод Польгаузена в первоначальном виде: в расчетные уравнения ( 4 - 20) и ( 4 - 21) входит явно вторая производная скорости внешнего потока по продольной координате. [9]
Уравнение ( 8 - 6) позволяет найти поле направлений на фазовом цилиндре. Действительно, производная скорости по углу геометрически интерпретируется как тангенс угла наклона касательной к фазовой кривой в данной точке. Линии, соединяющие точки фазового цилиндра с одним и тем же тангенсом угла наклона касательной, называют изоклинами. Нулевая изоклина соединяет точки, которые являются для фазовых кривых точками максимума, минимума или перегиба. [10]
Однако значения 0.015 и 0.005 нельзя, конечно, считать достаточно точными, так как для вычисления этих величин приходится находить производную скорости по данным в конечном числе точек. Причем в области отрыва производная скорости сильно меняется, а разброс в экспериментальных точках особенно велик. [11]
При постоянных давлении и температуре скорость пропорциональна [ 1 а ( А-1) ] г / 3, если определяющая стадия принадлежит внешней границе раздела. Поскольку по предположению Д - 1 0, производная скорости по а положительна и кривая превращения представляет собой зависимость с ускорением во времени. [12]
При постановке теоретической задачи необходимо сформулировать соответствующие физической реальности краевые условия для скоростей и их производных, входящих в уравнения движения жидкости. Это соответствует тому, что производная скорости по нормали к поверхности раздела фаз претерпевает излом, если коэффициенты вязкости жидкостей различны. [13]
Для определения распределения скорости отсасывания уравнение ( 9 - 6) решено методом изоклин. Польгаузена на случай отсасывания имеет тот же недостаток, что и метод К. Польгаузена в первоначальном виде: в расчетные уравнения ( 9 - 5) и ( 9 - 6) входит явно вторая производная скорости внешнего потока по продольной координате. Как отмечалось ранее, наличие и затрудняет расчет, поскольку при задании и ( х), например, в виде графика определение и i ( x) связано с немалыми трудностями и ошибками. [14]
Страницы: 1