Частная производная

Cтраница 3

Схема для вывода уравнения dS (. Применим. [31]

Частная производная от давления р использована потому, что давление, так же как и скорость и, является функцией двух переменных - I и I, а уравнение движения записано для определенного момента времени. [32]

Частная производная от внутренней энергии по времени dlf / dt заменяется в этом случае субстанциональной производной от энтальпии h по времени Dhjdt dh / dt f - V / h ( V - вектор скорости), причем Vyh представляет собой конвективную составляющую производной, в правой же части ур-ния ( 1) наряду с плотностью тепловых источников появляются члены, соответствующие работе сил давления ( сжатия) и теплоте, выделяющейся вследствие работы сил трения. [33]

Частная производная применена здесь потому, что температура изменяется не только по нормали к элементу dF, но и по другим направлениям, а в случае нестационарного поля еще, кроме того, зависит от времени. [34]

Частная производная dIJdUa показывает зависимость анодного тока от напряжения на аноде при постоянном сеточном напряжении и определяет величину проводимости участка анод - катод триода. [35]

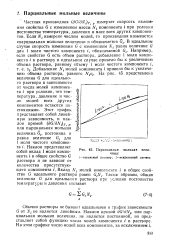Парциальная мольная величина. / - идеальный раствор. 2-неидеальный раствор. [36]

Частная производная ( dGldN T p измеряет скорость изменения свойства G с изменением массы N компонента i при условии постоянства температуры, давления и масс всех других компонентов. Если N [ измерено числом молей, то производная называется парциальная мольная величина и обозначается Gt. На рис. 45 представлена величина G для идеального раствора в зависимости от числа молей компонента i при условии, что температура, давление и число молей всех других компонентов остаются постоянными. [37]

Частная производная по времени от величины К отражает скорость изменения измеряемой величины. [38]

Частная производная df / dx равна той дополнительной продукции, которая может быть получена при увеличении количества t - ro ресурса на единицу. [39]

Частная производная dF / dxh пропорциональна косинусу, образуемому вектором градиента с г-й осью координат. [40]

Частная производная, полученная дифференцированием по различным переменным, называется смешанной частной производной. Частная же производная, полученная дифференцированием только по одной переменной, называется чистой частной производной. [41]

Частная производная от дополнительной работы по обобщенной силе равна соответствующему этой силе обобщенному перемещению. [42]

Частная производная dF / dxh пропорциональна косинусу, образуемому вектором градиента с г-й осью координат. [43]

Частная производная, стоящая множителем при ошибке-скаляре, не есть случайная величина, ее математическое ожидание равно самой величине. [44]

Частная производная, стоящая при модуле векторной ошибки, зависит от направления вектора. Векторными ошибками являются эксцентриситеты и перекосы осей шарниров, цилиндрических и винтовых пар, перекосы поступательных пар, перемещение в силу наличия зазоров в шарнирах, цилиндрических и поступательных парах. Если направление векторной ошибки имеет случайный характер, то и частная производная будет случайной величиной. [45]

Страницы: 1 2 3 4