Четвертая производная

Cтраница 1

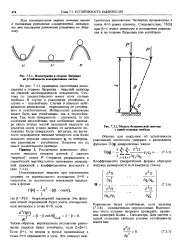Иллюстрация к теореме Лагранжа об устойчивости консервативных систем.| Модель механической системы с одной степенью свободы. [1]

Четвертая производная в точке 60 равна единице. Следовательно, П ( 6) при Р1 имеет минимум в положении равновесия и по теореме Лагранжа оно устойчиво. [2]

Четвертая производная от резонансной кривой осциллирует весьма специфическим образом. Гораздо более тонкий подход к изучению резонансной области вы найдете в работе Корнуэлла, Корригана и Нортона [16]; см. также следующий раздел. [3]

Если четвертая производная, вычисленная по формуле (11.105), оказывается слишком большой, то шаг сетки уменьшается и процесс решения повторяется. [4]

Если предположить, что четвертая производная практически постоянна, то снова можно применить экстраполяци-онный переход к пределу и улучшить результаты интегрирования по методу Симпсона. Вообще говоря, подобно тому, как была выведена формула (6.22), можно повышать точность, проводя через последовательные ординаты многочлены более высоких степеней. [5]

Гораздо точнее, разумеется, оказывается четвертая производная, вследствие ее большей крутизны. [6]

Затем нужно было бы каким-нибудь образом определить, где эта четвертая производная имеет максимум. [7]

Заметьте, что, хотя S ( /) основана на интерполяции степени два, в выражение погрешности входит четвертая производная и, следовательно, формула Симпсона точна для кубических функций. Другими словами, как и формула прямоугольников, формула Симпсона получает один дополнительный порядок точности. Читатель может проверить, что формула Симпсона точна в случае кубических функций. [8]

Следовательно, формула Симпсона имеет четвертый порядок точности с очень малым численным коэффициентом в остаточном члене. Формула Симпсона позволяет получить высокую точность, если четвертая производная подынтегральной функции не слишком велика. В противном случае методы второго порядка могут дать большую точность, чем метод Симпсона. [9]

Таким образом, на вход первого интегратора ( элемент 2) должна подаваться величина пятой производной. Очевидно, в этом случае с выхода первого интегратора снимается четвертая производная. [10]

Эта сушилка обладает наибольшим числом основных признаков, характерных для одно - и двухвальцовых сушилок всего ряда, и состоит из шести узлов. Первая производная базовой сушилки ( табл. 36) - сушилка одно-вальцовая с погружением - имеет пять узлов унифицированных и только один индивидуальный. Вторая производная - сушилка одновальцовая с раскатывающими валиками - имеет три унифицированных узла с основанием и четыре индивидуализированных. Третья производная - сушилка двух-вальцовая с наносными валиками - имеет четыре узла унифицированных и два индивидуализированных. Четвертая производная - сушилка двух-вальцовая с погружением - имеет три унифицированных узла с основанием и три унифицированных узла с другими производными, не имея при этом ни одного индивидуализированного узла. Пятая производная - сушилка двухвальцовая с раскатывающими валиками - имеет три унифицированных узла с основанием, два унифицированных узла второй производной и два индивидуализированных узла. [11]

Вторая производная от у по z - есть момент, взятый в масштабе жесткости. Если продифференцировать это выражение еще раз по z, то при постоянной жесткости EI получим поперечную силу Q. И наконец, четвертая производная от у по z дает нам интенсивность распределенной нагрузки q в масштабе жесткости. [12]

Страницы: 1