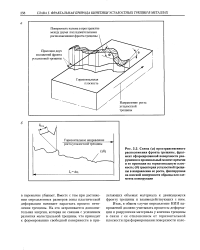
Процесс - ветвление
Cтраница 2
Правило ветвления Bf описывает процесс ветвления в задаче о перестановках. [16]
Как и в ВВС, процесс ветвления организуется таким образом, чтобы, пока это возможно, продолжить набор вершин в ту же группу Nr, что и на предыдущей итерации. [17]
Для реализации данного метода используется процесс ветвления по множеству переменных xrv в соответствии со схемой, предложенной в предыдущих задачах. [18]
Правило ветвления, которое определяет процесс ветвления по отношению к дереву поиска; назначение правила заключается в разбиении пространства решений на непересекающиеся подмножества, которые либо подвергаются дальнейшему исследованию, либо отбрасываются. [19]
Такая модификация выполняется на каждом шаге процесса ветвления. Полученный список обычно называют списком задач-кандидатов. Задача решена, если список задач-кандидатов пуст, т.е. если все они отсеяны по правилам отсева. [20]
Определим оценки множества решений задачи в процессе ветвления по данной схеме. Для этого предварительно докажем ряд утверждений. [21]
В работе [32] отмечается, что на процессы ветвления и структурирования оказывает влияние изомерия ароматического ядра кислотной компоненты. На термические превращения полиарилатов [32] ( а также полиимидов [33-34]) влияют не только строение входящих в цепь группировок, но и их взаимное расположение. Так, полиарилаты на основе 4 4 -дифенилфталиддикарбоновой кислоты термически более устойчивы, чем соответствующие им изомеры ( по положению лактонного цикла относительно карбонильной группы) на основе фенолфталеина как в условиях динамического, так и изотермического нагревания: разница в температурах начала разложения на воздухе составляет 50 - 60 С. [22]
В конце второго плато фрактальной размерности начинается процесс ветвления продольной складчатой структуры, который ведет к формированию вихревой структуры Формирование вихревой структуры соизмеримой с поперечным сечением образца приводит к его разрушению. [23]
Это, однако, не приводит в процессе ветвления к взаимно исключающим подзадачам. [24]
Далее, согласно схеме метода, переходим к процессу ветвления задачи. [25]
При этом, если указанные ограничения нарушаются, то процесс ветвления из таких вершин в дальнейшем не рассматриваем. Из вершин, удовлетворяющих указанным ограничениям, выбираем вершину Qv с минимальной оценкой. [26]
Разбиение множества на подмножества производится фиксированием значения XL В процессе ветвления на А - м шаге оценки подмножеств вычисляются по формуле ( 7 - 8) с учетом изменения множеств У0 и z0 за k - 1 шагов. [27]
Всего решено шесть подзадач, оптимум был известен до начала процесса ветвления, но для доказательства оптимальности начального решения выполнено три ветвления. [28]
Решение данного алгоритма основано на методе ветвей и границ, а сам процесс ветвления начинается с одной из моделей, имеющей максимальное число связей с другими. [29]
Страницы: 1 2 3 4