Процесс - вытекание - ртуть
Cтраница 1
Процесс вытекания ртути из капилляра приводит к возникновению тангенциальных движений поверхности, которые при достаточно большой скорости обусловливают ощутимое возрастание тока, тем более сильное, чем больше скорость движения поверхности. [1]
Движение внутри самой ртутной капли, вызываемое процессом вытекания ртути из капилляра, также приводит к перемешиванию раствора и возникновению максимумов второго рода. На неподвижных твердых электродах могут возникать максимумы третьего рода, которые связаны с повышенной скоростью наложения напряжения на РКЭ. [2]
В зависимости от факторов, вызывающих тангенциальные движения ртути, полярографические максимумы разделяют на максимумы 1-го рода, связанные с неравномерной поляризацией поверхности капли ртути, и максимумы 2-го рода, связанные с процессом вытекания ртути из капилляра. [3]
В зависимости от факторов, вызывающих тангенциальные движения ртути, полярографические максимумы разделяют на несколько видов: максимумы 1-го рода, связанные с неравномерной поляризацией поверхности капли ртути; максимумы 2-го рода, связанные с процессом вытекания ртути из капилляра. В настоящее время выявлены также и максимумы 3-го рода, которые обусловлены тангенциальными движениями, вызываемыми неравномерной адсорбцией органических веществ на поверхности ртутной капли; эти максимумы детально изучены в [319, 320], но применение их для исследования высокомолекулярных веществ еще не известно. [4]
Появление максимумов, как показали специальные исследования - следствие перемешивания раствора за счет движения поверхности ртутной капли. Последнее вызвано прежде всего самим процессом вытекания ртути из капилляра. Взаимодействие заряженной поверхности ртутной капли с электрическим полем также вызывает дополнительное движение поверхности; ртути. [5]
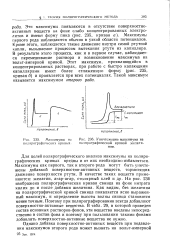 |
Максимумы на полярографических кривых.| Уничтожение максимума на полярографической кривой желати. [6] |
Максимумы первого рода наблюдаются обычно в узкой области потенциалов. Кроме этого, наблюдается также движение внутри самой ртутной капли, вызываемое процессом вытекания ртути из капилляра. В результате этого процесса, как и в первом случае, наблюдается перемешивание раствора и возникновение максимума на вольт-амперной кривой. Этот максимум, проявляющийся в концентрированных растворах, при работе с быстро капающими капиллярами имеет более сглаженную форму ( рис. 235, кривая б) и проявляется при всех потенциалах. Такой максимум называется максимумом второго рода. [7]
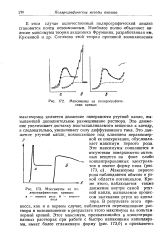 |
Максимумы на полярографических кривых.| Максимумы на полярографических кривых. [8] |
Максимумы первого рода наблюдаются обычно в узкой области потенциалов. Кроме этого, наблюдается также движение внутри самой ртутной капли, вызываемое процессом вытекания ртути из капилляра. В результате этого процесса, как и в первом случае, наблюдается перемешивание раствора и возникновение в результате этого максимума на вольтам-перной кривой. [9]
Движение ртутной капли, возникающее под влиянием неравномерной ее поляризации, обусловливает максимум первого рода. Максимумы первого рода наблюдаются обычно в узкой области потенциалов. Кроме этого, наблюдается также движение внутри самой ртутной капли, вызываемое процессом вытекания ртути из капилляра. [10]
Важным по своим многочисленным приложениям разделом диффузионной кинетики является полярография. Здесь в первую очередь следует назвать разработку теории полярографических максимумов. Кроме того, Т. А. Крюковой был открыт новый вид полярографических максимумов, так называемые максимумы второго рода, связанные с самим процессом вытекания ртути. Развитая ранее за рубежом теория полярографических волн была применима лишь к обратимым реакциям. [11]
Важным по своим многочисленным приложениям разделом диффузионной кинетики является полярография. Здесь в первую очередь следует назвать разработку теории полярографических максимумов. Кроме того, Т. А. Крюковой был открыт новый вид полярографических максимумов, так называемые максимумы второго рода, связанные с самим процессом вытекания ртути. Развитая ранее за рубежом теория полярографических волн была применима лишь к обратимым реакциям. [12]
Страницы: 1