Процесс - грам
Cтраница 1
Процесс Грама - Шмидта состоит в следующем. [1]
Процесс Грама - Шмидта может быть истолкован как разложение невырожденной квадратной матрицы в произведение ортогональной ( или унитарной матрицы в случае эрмитова пространства) и верхней треугольной матрицы с положительными диагональными элементами, что есть частный случай Ивасавы разложения. [2]
Процесс Грама - Шмидта может быть истолкован как разложение невырожденной квадратной матрицы в произведение ортогональной ( в эрмитовом случае - унитарной) и верхней треугольной матрицы с положительными диагональными элементами. Он может быть использован для решения системы линейных алгебраич. [3]
 |
Подпространства пространства. [4] |
Используя процесс Грама - Шмидта или иным способом, построить ортонормальиые базисы заданных в § 11.1 подпространств. [5]
Доказать существование QR - разложения в случае неполного ранга, модифицировав процесс Грама - Шмидта так, чтобы учесть возможность появления нулевых векторов. [6]
Мы не считаем, что новая и более элементарная формула ( 56) будет удобнее для вычислений, чем ( 52) или процесс Грама - Шмидта. [7]
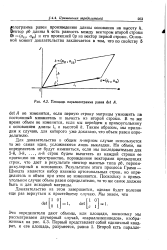 |
Площадь паралелограмма равна det A. [8] |
Для доказательства в общем n - мерном случае используется та же самая идея, усложняются лишь выкладки. Результатом этого процесса Грама - Шмидта является набор взаимно ортогональных строк, но определитель и объем при этом не изменяются. Поскольку в прямоугольном случае объем равен определителю, то то же самое должно быть и для исходной матрицы. [9]
Этим заканчивается описание процесса Грама - Шмидта. [10]
В доказательстве нам необходима ортогональная матрица Q. Хороший способ выбора Q доставляет применение процесса Грама - Шмидта к столбцам матрицы С. [11]
Для исправления этой ситуации применяется процесс переортогонализации. ОРТОГОНАЛИЗАЦИЯ, процесс ортогоналя-заци и, - алгоритм построения для данной линейно независимой системы векторов ( в евклидовом или эрмитовом пространстве V) ортогональной системы векторов, порождающих то же самое подпространство в V. Наиболее известным является процесс Грама - Шмидта, состоящий в следующем. Пусть задана система векторов Oj. Полагают 6joi, далее построение ведется индуктивно. [12]
Если Vk 0, то мы удаляем н из С и продолжаем построение. Легко видеть, что множество В ортонормально. Этот способ построения ортонор-мальных множеств называется процессом Грама - Шмидта. [13]
Любая матрица, например размера 4x4, имеет по крайней мере одно собственное значение Хг; в наихудшем случае оно будет повторяться четыре раза. Мы нормализуем х к единичному вектору xt и помещаем его в первый столбец матрицы U. На этом этапе определить остальные три столбца невозможно, и мы заполняем их произвольным образом, но так, чтобы получившаяся матрица б была унитарной. Процесс Грама - Шмидта гарантирует осуществимость этого. [14]
Целью этой книги является рассмотрение некоторых прикладных разделов теории матриц. Излагаемая здесь теория принципиально ничем не отличается от стандартных курсов абстрактной линейной алгебры, но сейчас для нас самое главное, что рассматриваемая теория действительно важна для приложений. Разница состоит в том, что переместился центр тяжести в соответствии с новой точкой зрения. Метод исключения Гаусса - это теперь не только способ нахождения базиса пространства строк, а процесс Грама - Шмидта-не просто способ доказательства, что каждое подпространство имеет ортонормированный базис. Напротив, нам действительно нужны эти алгоритмы и нужно удобное описание ( А LU или А QR) того, что они делают. [15]
Страницы: 1 2