Апериодический процесс
Cтраница 4
Кривые рис. Д-5, в изображают затухающие апериодические процессы в цепи второго порядка при различных начальных условиях. [46]
При ах а2 получается решение для апериодического процесса. При удовлетворительно выполненных подшипниках ( k невелико) at о2 так что корни PJ и р3 являются комплексными и колебания получаются затухающими. [47]
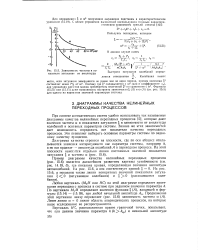 |
Зависимость частоты и показателя затухания от амплитуды. [48] |
Левее линии ш 0 лежит область апериодических процессов, на которые наше исследование не распространяется. [49]
При % я2 получается решение для апериодического процесса. При удовлетворительно выполненных подшипниках ( k невелико) aL а2, так что корни р1 и р2 являются комплексными и колебания получаются затухающими. [50]
Кривые 3 и 6 даны для апериодического процесса, кривые 2 и 5 - для 20-процентного перерегулирования, кривая 4 показывает минимальное значение интеграла от квадрата отклонения регулируемого параметра, кривая 7 - 40-процентное перерегулирование. [51]
Страницы: 1 2 3 4