Алгоритмический процесс
Cтраница 1
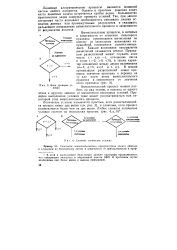 |
Сложное логическое условие. [1] |
Линейные алгоритмические процессы являются основной частью любого алгоритма. Однако в практике решения задач чисто линейные задачи встречаются крайне редко. [2]
Разветвляющийся алгоритмический процесс разбивается на ряд шагов Некоторые из них могут иметь несколько преемников. [3]
Состояниями алгоритмического процесса являются колмогоропгкщ комплексы из некоторого ансамбля ( Б, й) - комплексов. [4]
Линейным называется такой алгоритмический процесс, при котором все этапы решения задачи выполняются в естественном порядке следования записи этих этапов. [5]
Ветвящимся называется такой алгоритмический процесс, в котором выбор направления, а значит, и характера обработки информации зависит от результатов проверки выполнения какого-либо логического условия. Каждое отдельное направление обработки информации называется ветвью. Для данной алгоритмической структуры характерно, что в любой конкретный момент ее реализации осуществляется обработка только по одной из ветвей, а выполнение операции по другим ветвям исключается. Учитывая эту специфику, для обеспечения корректности разработки алгоритма решения конкретной задачи контрольный пример должен содержать данные, предусматривающие проверку всех ветвей алгоритма. [6]
Так как требование завершения алгоритмического процесса за конечное число шагов не учитывает реальных возможностей, связанных с затратами времени и расходованием ресуров, то говорят, что при этом алгоритм потенциально ( а не реально) выполним. [7]
Описание основных принципов организации алгоритмического процесса в универсальных электронных цифровых машинах дает общее представление о так называемой блочной структуре подобных машин. При реальном проектировании электронных программных автоматов этап блочного синтеза является лишь исходной точкой для разработки тех или иных схемных решений. Выбор этих решений осуществляется на основе теории автоматов и теории комбинационных схем, изложенных в гл. [8]
Заметим, что в ходе алгоритмического процесса возможно исчезновение или появление некоторых элементов операнда. [9]
Дискретность алгоритма означает возможность разбиения определенного алгоритмического процесса на отдельные элементарные этапы, возможность реализации которых человеком или ЭВМ не вызывает сомнения, а результат выполнения каждого элементарного этапа вполне определен и понятен. Таким образом, алгоритм дает возможность чисто механически решать любую конкретную задачу из некоторого класса однотипных задач. [10]
В приведенных выше примерах алгоритмы порождают четко видимые алгоритмические процессы, каждый шаг которых очень прост. Если алгоритм к какому-либо допустимому исходному данному неприменим, то алгоритмический процесс может для этого исходного данного либо продолжаться неограниченно ( быть бесконечным), либо безрезультатно обрываться. [11]
Возможен еще один тип безрезультатной остановки алгоритмического процесса, когда таблица соответствия содержит не все возможные для данного алгоритма виды активных зон. [12]
Что же касается относительной эффективности каждого алгоритмического процесса, то замечания, приведенные в гл. В частности, при а 1 метод итераций по критерию обладает преимуществом, связанным с простотой численных приемов, но в то же время страдает таким недостатком, как отсутствие конечной сходимости. Достоинством метода итераций по стратегии является сходимость за конечное число итераций, однако объем вычислений на каждой итерации возрастает, поскольку приходится решать полную систему однородных линейных уравнений. Довольно просто можно объединить эти две схемы в единый комбинированный алгоритм. Преимущество применения метода линейного программирования заключается в том, что можно воспользоваться широко распространенными сложными программами решения задач линейного программирования на ЭВМ, не говоря уже о том, что использование симплексного метода решения двойственных задач, приведенных в разд. В частности каждая итерация симплексного-метода соответствует улучшению стратегии только в единственном состоянии, а не во всех состояниях, где в принципе возможно какое-либо улучшение. [13]
Принципиальная блок-схема алгоритма должна отражать этапность алгоритмического процесса. Этапность изображается в виде блоков ( совокупность процедур решения задач) с указанием взаимной связи. Внутри каждого блока кратко описывается содержание соответствующего этапа алгоритма с использованием принятых в данной задаче условных обозначений реквизитов. Символы ( условные обозначения) реквизитов применяются с индексом массива ( цифровая часть шифра массива), из которого берется значение реквизита. Блоки нумеруются арабскими цифрами над правым верхним углом. [14]
Какие операторы языка описывают основные типы алгоритмических процессов. [15]
Страницы: 1 2 3 4