Множественный процесс
Cтраница 1
Множественные процессы) [4], к-рые в силу условия унитарности определяют мнимые части амплитуд двухчастичных процессов. Взаимодействие адронов является наиб. [1]
 |
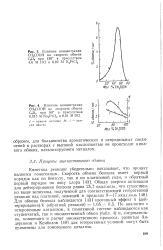
Флуктуации электронно-фотонных каскадов при разных вч в Fe.| Электронно-ядерный ливень, зарегистрированный в пузырьковой камере. Стрелкой отмечено начало ливня. [2] |
Множественные процессы), причем / з от полного числа рожденных пионов составляют нейтральные пионы, дающие после распада начало электронно-фотонному каскаду. [3]
Ферми угловые и энергетические распределения множественных процессов основываются на законах сохранения энергии и импульса. [4]
& й), и множественных процессов ударной ионизации, в к-рых образуются новые электронно-дырочные пары. При этом т 1, однако 4 fi ( af8g, Последнее связано с необходимостью сохранения импульса в элементарных актах рождения электронно-дырочных пар с возбуждением колебаний решетки. [5]
Гейзенберг интерпретирует этот снимок как свидетельство в пользу множественных процессов, но с тем же успехом это может быть и ливень, в котором случайно все тяжелые частицы оказались нейтронами. [6]
Наиб, полно это было сделано А. А. Логуновым и др. для множественных процессов с выделенными частицами - инклюзивных процессов. Для них были, в частности, найдены асимптотич. Серпухов, 1968) привело к установлению явления масштабной инвар иантиости. [7]
От энергии сталкивающихся частиц оказывается практически не зависящим также распределение по числу частиц, образующихся в множественном процессе. В этом случае вероятность рождения п частиц пропорциональна ф-ции лишь от отношения п / п), где ( га) - ср. [8]
При увеличении энергии сталкивающихся частиц возникает возможность образования многих частиц в одном акте столкновения. Особенно интересны множественные процессы с участием мезонов. [9]
Сложная картина возникает при взаимодействии быстрых частиц с веществом. Для получения информации о множественных процессах и объектах, которые в них участвуют, требуется создание многотонных пузырьковых камер, размещаемых в магнитных полях. Определение большого времени жизни частиц или ядер требует длительных измерений на стабильной регистрирующей аппаратуре в условиях малого фона, а следовательно, с привлечением необходимой активной и пассивной защиты. [10]
Однако в известной степени близко к кинематике подходит высказанная Ферми идея о том, что характеристики множественных процессов, приводящих к образованию ядерно-активных частиц, определяются статистическим весом конечных состояний. Подробный обзор статистической теории выходит за рамки этой книги. [11]
Логико-математические основы факторного анализа были рассмотрены в гл. Подчеркнем лишь, что их отличие от моделей, строящихся на множественной регрессии, связано с фундаментальной проблемой биологии старения: гомеоклаз - это унитарный или множественный процесс. В первом случае регрессионные модели позволяют одной величиной ( индексом биологического возраста) оценить то, что действительно едино; во втором случае такая оценка не больше, чем практически удобный прием, ради модельной простоты игнорирующий организационную сложность старения. Факторные модели БВ строятся таким образом, что позволяют выявить множественность возрастных процессов только в том случае, если она есть в реальности. В отличие от подхода, опирающегося на множественную регрессию, факторный анализ не связан ни с какими предварительными предположениями об одномерности или многомерности старения. [12]
Кинетика реакции убедительно показывает, что процесс является гомогенным. По аналогии с гетерогенным катализом, в гомогенной системе наблюдаются как ступенчатый, так и множественный обмен ( табл. 4) и, следовательно, концепция и расчет множественного процесса, развитые Андерсоном и Кемболом [49] для гетерогенных условий, могут быть применены для гомогенного катализа. [14]
 |
Множественное рождение адронов при столкновении. [15] |
Страницы: 1 2