Экспериментальная прямая

Cтраница 3

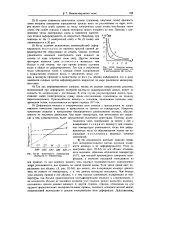
Схема и порядок распределения параметров распределений. а - нормального. б - Вейбулла с помощью сеток интенсивности. [31]

Затем через точку А сетки интенсивности проводят луч, параллельный экспериментальной прямой, до его пересечения в точке С с вертикальной линией Я. [32]

Энергия взаимодействия однозарядных ( А и двухзарядных ( Б частиц. [33]

С другой стороны, отрезки, отсекаемые на оси ординат продолжениями экспериментальных прямых, являются непосредственной мерой, испытываемой молекулами в данном электрическом поле деформации. [34]

Рассмотрим сначала метод Вертело. Уже Кат и Камерлинг-Оннес [16] при рассмотрении данных по кислороду, азоту и аргону показали, что наклон экспериментальной прямой в координатах d ( pv) / dp и 1 / Т2 отличается от того наклона, который следует из уравнения Вертело. [35]

Как видно из графика и табл. 4, экспериментальные точки располагаются вдоль прямых, близких к теоретическим. Поскольку принятые при выводе уравнения ( 18, III) допущения для опытов Д. С. Вилькера являются достаточно точными, некоторое несовпадение теоретических и экспериментальных прямых указывает на то, что остаточное давление по Вилькеру несколько отличается от среднего давления. [36]

Зависимость значений. [37]

Коэффициент корреляции данной Зависимости равен 0 96, что указывает на очень тесную связь между износом рабочих поверхностей плунжерной пары и распылителя форсунки. При этом экспериментальная прямая не проходит через начало координат, так как в начальный период работы интенсивность изнашивания рабочих поверхностей плунжера и втулки невелика, в то время как эффективное проходное сечение распылителей форсунок существенно изменяется вследствие скругления кромок сопловых отверстий. Учитывая, что трудоемкость контроля параметров распылителя форсунки ниже, чем параметров плунжерной пары, при значительно меньшей погрешности, можно сравнительно оценивать эффективность работы топливных фильтров в условиях эксплуатации путем контроля технического состояния распылителей форсунок. [38]

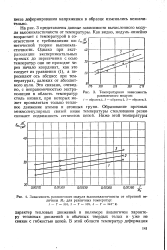Температурная зависимость.| Зависимость равновесного модуля высокоэластичностн от обратной величины Мс для различных температур. [39]

На рис. 3 представлены данные зависимости вычисленного модуля высокоэластичнОсти от температуры. Как видно, модуль линейно возрастает с температурой в соответствии с требованиями ки-нетической теории высокоэластичности. Однако при экстраполяции экспериментальных прямых до пересечения с осью температур они не проходят через начало координат, как это следует из уравнения ( 1), а пересекают ось абсцисс при температурах, далеких от абсолютного нуля. Это связано, очевидно, с неправомочностью экстраполяции в область температур столь низких, при которых может проявляться только тепловое движение атомов и атомных групп. Образование прочных межмолекулярных связей ниже температуры стеклования резко снижает подвижность сегментов цепей. [40]

Из него следует линейная зависимость между величиной еЬ з и частотой v света. На рис. V.5.3 приведены экспериментальные прямые, выражающие зависимость eU3 от частоты v для фотоэффекта на нескольких металлах. [41]

Из него следует линейная зависимость между величиной eU3 и частотой У света. На рис. V.5.3 приведены экспериментальные прямые, выражающие зависимость eU3 от частоты у для фотоэффекта на нескольких металлах. [42]

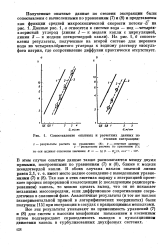Сопоставление опытных и расчетных данных по. [43]

В этом случае опытные данные также располагаются между двумя прямыми, построенными по уравнениям ( 7) и ( 8), ближе к модели псевдотвердой капли. Так как в этих системах наряду с экстракцией протекает процесс непрерывной коалесценции ( с последующим редисперги-рованием) капель, то можно сделать вывод, что он не искажает механизма массопередачи, если диффузионное сопротивление сосредоточено в сплошной фазе. Аналогичные результаты ( и тот же наклон экспериментальной прямой в логарифмических координатах) были получены [15] при экстракции в сосудах с вращающимися мешалками. Все эти результаты указывают на применимость уравнений ( 7) и ( 8) для систем с высоким межфазным натяжением и косвенным путем подтверждают справедливость выводов о пульсационном движении капель в турбулизованных двухфазных системах. [44]

Соединенные пунктиром точки отвечают экспериментальным данным. Как видно из графика и табл. 4, экспериментальные точки располагаются вдоль прямых, близких к теоретическим. С, Вилькера являются достаточно точными, некоторое несовпадение теоретических и экспериментальных прямых указывает на то, что остаточное давление по Вилькеру несколько отличается от среднего давления. [45]

Страницы: 1 2 3 4