Пучок - прямая
Cтраница 3
Здесь через точку М проведен пучок прямых, пересекающих кривую АВ. Через середины хорд проведена кривая ab - кривая ошибок. Эта вспомогательная кривая пересекает данную кривую А В в точке С. Прямая СМ является касательной. [31]
Проведя теперь из начала координат пучок прямых до пересечения с зависимостью v ( n) и соединив середины полученных хорд плавной линией, получаем искомую кривую минимально возможных механических скоростей бурения при наличии автоколебательного процесса бурильной колонны. Область, расположенная между кривыми линиями v ( n) и vcmin ( n) ( на рис. 4.9 она заштрихована), является областью возможных значений механических скоростей бурения. Отметим, что в случае идеальной промывки забоя ( практически вся выбуренная борода удаляется с забоя скважины) кривые vc min и v ( n) совпадают, так как в этом случае имеет место линейная зависимость между механической скоростью бурения и скоростью вращения долота, а потому номинальное значение механической скорости и значение ее при крутильных автоколебаниях совпадают. [32]
Все сказанное при исследовании уравнения пучка прямых ( п 3 § 48) непосредственно переносится и на случай пучка плоскостей. [33]
Пучок или связка прямых проецируется в пучок прямых, причем центр пучка или связки проецируется в центр пучка. [34]
Пучок или связка прямых проецируется в пучок прямых, причем центр пучка или связки проецируется в центр пучка проекций прямых. Множество проецирующих прямых, касающихся поверхности тела ( например, SALLTI), представляет собой коническую проецирующую поверхность. [35]
Пучок или связка прямых проецируется в пучок прямых, причем центр пучка или связки проецируется в центр пучка проекций прямых. [36]
Проекции, для получения которых используется пучок прямых, не перпендикулярных плоскости экрана, принято называть косоугольными. [37]
В частности, взаимно однозначное соответствие пучка прямых и пучка плоскостей может быть, очевидно, установлено через посредство прямолинейного ряда точек. [38]
Уравнение ( 1) называют уравнением пучка прямых, заданного образующими. [39]
Стороны АС и ВС описывают два пучка прямых 2-го порядка, перспективные двум когруэнтным рядам, описываемым точками Л и Б, поэтому эти два пучка проективны, но они имеют один и тот же носитель - касаются одной окружности, потому точки пересечения их соответствующих прямых будут образовывать кривую 2-го порядка. [40]
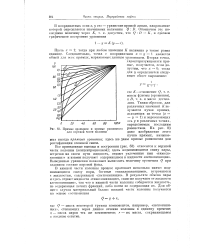 |
Прямые орошения и кривые равновесия для верхней части колонны. [41] |
Таким образом, для различных значений получается пучок прямых, исходящих из точки ( х у 1) и пересекающих ось у в различных точках, определяемых последним равенством. На рис. 83 дано изображение этого пучка прямых, называемых иногда прямыми орошения; здесь же даны кривые равновесия для ректификации сложной смеси. [42]
При постоянных значениях k это уравнение определяет пучок прямых, проходящих через начало координат. [43]
Одно из определений RP3 реализует его как пучок прямых в R4, проходящих через О. [44]
 |
Картина распределения токов в резонаторе при колебаниях типа Ям.| Диаграмма настройки. [45] |
Страницы: 1 2 3 4