Пучок - вектор
Cтраница 1
Пучок векторов с R O всегда принадлежит третьему подклассу, так как M0 Q, если выбрать О в центре пучка. Но Aft не зависит от выбора полюса, и условия R. Q, Mi Q для такого пучка заведомо выполнены. [1]
Что понимается под помехоустойчивостью пучка векторов. Какие пучки обладают наибольшей помехоустойчивостью. [2]
Параметром кривых является угол а расхождения пучка векторов самопроизвольной намагниченности. Если имеются внутренние напряжения, то расхождение пучка сужается, так как выделяется направление легкого намагничивания. Кривые соответствуют случаю, когда направление легкого намагничивания совпадает с направлением действующей измеряемой силы. [3]
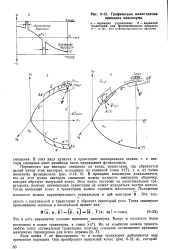 |
Графическая иллюстрация принципа максимума. [4] |
В принципе максимума доказывается, что на этот пучок векторов смещения можно натянуть выпуклую оболочку, которая образует выпуклый конус. Этот конус построен на неоптимальных траекториях, поэтому оптимальная траектория не может находиться внутри конуса. [5]
Преобразования, связанные с добавлением или отбрасыванием векторных нулей и с заменой пучка векторов одним вектором, назовем элементарными преобразованиями. [6]
Если отложить от произвольной точки, как из центра по направлениям радиуса, выражения ап sin2 ссг - и & nsin2a, то получим пучок векторов. Очевидно, направление равнодействующей, принадлежащей векторам п-и гармоники, будет отличаться друг от друга в зависимости от номера гармоники. В силу этого при вращении ротора будут возникать последовательно плоскости изгиба ротора, совпадающие с направлением равнодействующих гармонических составляющих, согласованных с критическими скоростями гибкого ротора. [7]
В данной главе были рассмотрены различные аспекты решения задачи, связанной с вращением пространственно заданного пучка радиус-векторов, описываемых кватернионным сигналом. По сравнению с плоским вариантом данной задачи кроме угла поворота в процессе вращения необходимо учитывать положение оси, вокруг которой поворачивается пучок векторов. Таким образом, сама задача анализа поворота трехмерного сигнала из одномерной стала многомерной. Наиболее важные результаты ее решения состоят в следующем. [8]
Если дана система материальных точек и некоторый центр О, то, определив моменты количеств движения каждой материальной точки относительно этого центра, получим пучок векторов, пересекающихся в центре О. [9]
Если дана система материальных точек и некоторый центр О, то, определив моменты количеств движения всех материальных точек относительно этого центра, получим пучок векторов, пересекающихся в центре О. [10]
Страницы: 1