Пять - число
Cтраница 1
Пять чисел х, у, rf, d, k y или ж, р, т, а, г у служат грубой характеристикой распределения экспериментальных точек на плоскости. [1]
Первые двадцать пять чисел этой последовательности могут по всей справедливости рассматриваться как номера выпускников, которым посчастливилось получить путевку. Впрочем, с тем же основанием могли быть выбраны последние двадцать пять чисел последовательности. [2]
Вычеркнув эти пять чисел, мы оставим 2 - е, 5 - е и 6 - е числа, или же 7 - е, 4 - е и 3 - е числа. Рассмотрим сначала первый случай. Следовательно, если эти три числа не делятся ни на 3, ни на 5, то одно из них ( а именно, то, которое не делится ни на 7, ни на 11) будет взаимно просто со всеми остальными числами. Точно так же проводится доказательство и в том случае, когда после вычеркивания чисел, делящихся на 3 и на 5, остаются 3 - е, 4 - е и 7 - е числа. [3]
Вычеркнув эти пять чисел, мы оставим 2 - е, 5 - е и 6 - е числа, или же 7 - е, 4 - е, и 3 - е числа. Рассмотрим сначала первый случай. Следовательно, если эти три числа, не делятся ни на 3, ни на 5, то одно из них ( а. Точно так же проводится доказательство и в том случае, когда после вычеркивания чисел, делящихся на 3 и на 5, остаются 3 - е, 4 - е и 7 - е числа. [4]
В памяти находятся пять чисел. [5]
Значения простых переменных ( пять чисел) и элементов массива ( четыре числа) в указанном порядке должны содержаться во вводном устройстве, например быть набитыми на перфокарты. [6]
Результаты выводятся на печать по пять чисел в одной строке в формате с фиксированной точкой. Каждое число занимает пять по-еиций. [7]
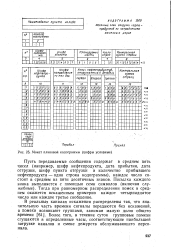 |
Макет плановой кодограммы ( цифры условные. [8] |
Пусть передаваемые сообщения содержат в среднем пять чисел ( например, шифр нефтепродукта, дата прибытия, дата отгрузки, шифр пункта отгрузки и количество прибывшего нефтепродукта - одна строка кодограммы), каждое число состоит в среднем из пяти десятичных знаков. Тогда при равномерном распределении помех в среднем окажется искаженным примерно каждое четырнадцатое число или каждое третье сообщение. [9]
Между числами 1 и 25 напишите пять чисел, которые с данными числами образуют арифметическую прогрессию. [10]
Из цифр 1 и 2 составлено пять 100-значных чисел; при этом известно, что у каждых двух чисел ровно в г разрядах совпадают цифры, однако ни в одном разряде не совпадают все пять цифр. [11]
Чтобы правильно указать на данной карточке ровно пять выигрышных чисел, нужно из шести счастливых чисел выбрать пять и добавить к ним одно из оставшихся 43 несчастливых чисел. [12]
 |
Счетчик оборотов. [13] |
Необходимо отметить, что при черновом режиме пять чисел двойных ходов повторяются. [14]
Четырехзначные числа в этой таблице сгруппированы в группы по пять чисел, расположенных столбиком, причем таких столбиков в каждом столбце страницы содержится десять и столбцов на странице также десять. Таким образом, на каждой странице помещается 5x10x10 500 четырехзначных чисел. [15]
Страницы: 1 2 3 4