Фрактальный анализ

Cтраница 1

Фрактальный анализ предлагает для моделирования более сложную математику, но его результаты гораздо ближе к практическому опыту. Фрактальная структура рынков капитала порождает циклы, тренды и множество возможных справедливых цен. Она привносит качества, делающие рынки капитала интересными, в том числе зависимость от человеческих решений, и делает возможным их измерение в количественном аспекте. Фрактальная статистика указывает на беспорядочность и сложность жизни, но многое таит в себе. [1]

Помимо фрактального анализа автор включает в рассмотрение экономическую динамику в аспекте качественной теории нелинейных дифференциальных уравнений - так называемый детерминированный хаос. Как перспективные направления исследований рассматриваются методы самоорганизованной критичности в применении к анализу коллективного поведения экономических субъектов и кризисным явлениям в экономике. В качестве инструментов прогнозирования экономических показателей кратко охарактеризованы методы нечеткой логики и нейронных сетей. [2]

Методами фрактального анализа временных рядов установлено, что колебания давления на забое фонтанных скважин имеют детерминированный характер. [3]

Для фрактального анализа пористых материалов наряду с методами адсорбции, рассмотренными в предыдущем пункте, применяют методы ртутной порометрии [107, 109], позволяющие находить интегральные функции распределения пор по V ( r) - объему пор радиусом г и более. [4]

Известно, что фрактальный анализ дает только математическое описание полимеров, т.е. он не определяет те структурные единицы ( элементы), из которых строится структура всякого полимера. [5]

В последние годы фрактальный анализ становится одним из основных методов характеризации шероховатости поверхностей различных твердых тел. Поэтому применение фрактального анализа для оценки рельефа диэлектрических слоев может явиться оптимальным методом контроля состояния поверхности тонких пленок. [6]

В последние годы фрактальный анализ становится одним из основных методов характеризации шероховатости поверхностей различных материалов. [7]

Первый раздел диссертации Фрактальный анализ динамики давления в скважине посвящен применению алгоритмов обработки временных рядов, разработанных в нелинейной динамике, к анализу динамики давления в нефтяных скважинах. Раздел содержит подразделы с теоретическими основами фрактального анализа, постановкой задачи и результатами расчетов и выводами. [8]

В основе эмпирических методов фрактального анализа лежит так называемый метод Херста, или ( R / S) - метод [ 1 ], ориентированный на выявление и оценку нестационарных компонент случайного процесса. [9]

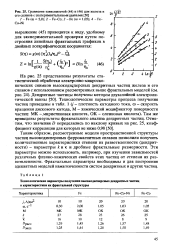Сравнение зависимостей ( 44 и ( 46 для железа и L ( I2. [10]

Там же приведены результаты фрактального анализа дендритных частиц. [11]

Метод преобразования подобия позволяет проводить фрактальный анализ по микрофотографиям полос скольжения, границ зерен, изображений поверхности разрушения. Вероятно, устойчивость структуры полос скольжения, образующихся в процессе усталости, указывает на проявление фрактальных свойств пластически деформируемого твердого тела. [12]

В статье А.В. Панина и А.Р. Шугурова Фрактальный анализ поверхностей тонких пленою) показана эффективность использования сканирующей атомно-силовой микроскопии для фрактального анализа рельефа поверхности тонких диэлектрических пленок. При напылении слоев SiO2 на полупроводниковую подложку ( GaAs) образуются квазипериодические дефектные мезоструктуры, проявляющиеся в форме гофра. [13]

Решение указанной задачи требует разработки фрактального анализа микроструктур и определении области существования структурного самоподобия, а также разработки фрактального синтеза, включающего моделирование характерных геометрических форм ( путем итераций) как способа для изучения начальных структур в реальных материалах. [14]

В работах [9, 10, 127] сформулирован принцип фрактального анализа микроструктур материалов, в основу которого положена теорема Рамсея. Согласно этой теореме, любое достаточно большое множество чисел или точек ( элементов структуры) обязательно содержит высокоупорядоченную структуру. Это означает, что любую структуру, содержащую достаточно большое количество элементов, можно рассматривать как мульти-фрактал, составленный из конечного числа вложенных друг в друга самоподобных структур. Однако фрактальный микроструктурный анализ, открывающий путь к количественной металлографии, методически пока остается сложной задачей. [15]

Страницы: 1 2 3 4