Статистическая радиофизика

Cтраница 1

Статистическая радиофизика занимается изучением стохастических явлений в колебательных и волновых процессах. В математическом плане дело сводится к решению линейных или нелинейных дифференциальных уравнений со случайными начальными ( или краевыми) условиями, случайными параметрами ( коэффициентами), случайными внешними силами - так называемых стохастических дифференциальных уравнений. [1]

В статистической радиофизике и оптике стационарные процессы занимают особенно важное место; условия их реализуемости осуществляются во многих экспериментальных ситуациях. Вместе с тем подчеркнем, чтэ и нестационарные процессы, для которых ( 50) несправедливо, также играют важную роль: например, все переходные процессы, протекающие в присутствии флуктуации, оказываются фактически нестационарными случайными процессами. [2]

Математической основой статистической радиофизики и оптики является теория случайных функций. [3]

Средняя частота пересечения огибающих двух независимых гауссовских процессов как функция отношения их дисперсий а С2 / 2 при отношении полос г 3. [4]

Математический анализ задач статистической радиофизики н оптики обычно сводится к решению линейных или нелинейных дифференциальных уравнений со случайными начальными ( или краевыми) условиями, случайными параметрами, коэффициентами, случайными внешними силами, - так называемых стохастических дифференциальных уравнений. [5]

Рыто в С. М. Введение в статистическую радиофизику. [6]

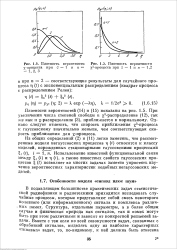Плотность вероятности.| Плотность вероятности Х2 - процесса прп а 1 ц и 1 2. [7]

В подавляющем большинстве практических задач статистической радиофизики и радиотехники приходится исследовать случайные процессы, которые представляют собой смесь некоторого полезного ( или информационного) сигнала и комплекса различных помех. [8]

В более широком смысле под статистической радиофизикой понимают круг задач, связанных с изучением статистических явлений в колебательных и волновых процессах, причем речь не обязательно идет об электромагнитных колебаниях и волнах. [9]

Рыто в, Кравцов Ю. А., Татарский В. И. Введение в статистическую радиофизику. [10]

Мы считаем своим приятным долгом выразить признательность С. М. Рытову и участникам руководимого им семинара по статистической радиофизике; многолетнее участие в этом семинаре оказало значительное влияние на формирование наших взглядов на статистическую радиофизику и ее преподавание. [11]

В задачах об интерференции и дифракции случайных волн две постановки вопроса представляют особый интерес для статистической радиофизики и оптики. С одной стороны, необходимы ясные представления о том, как изменяется характер интерференционных и дифракционных явлений, когда вместо регулярной волны мы имеем дело со случайными волнами. Этот аспект детально прослеживается в настоящей главе. [12]

Читаемый авторами в течение последних пятнадцати лет на физическом факультете Московского университета курс тяготеет скорее к статистической радиофизике в широком смысле. [13]

Заканчивая этот краткий вводный очерк, заметим, что с задачами, во многом сходными с задачами статистической радиофизики и оптики, приходится сталкиваться в гидродинамике, акустике и физике плазмы. Речь идет здесь о теории турбулентности ( см. [40, 43]), физике линейных и нелинейных ( см. [38]) случайных волн в акустике. [14]

Рассматриваемые ниже статистические задачи теории нелинейных волн в математическом плане, несомненно, относятся к наиболее сложным задачам статистической радиофизики. Поэтому в этой главе мы в полной мере используем математический аппарат, изложенный в гл. Наряду с усреднением аналитических решений ниже широко используются уравнения для средних, записанные в различных приближениях. [15]

Страницы: 1 2 3