Радиус - кривизна - эллипс
Cтраница 1
Радиус кривизны эллипса рэ при зацеплении зубьев в полюсе рэ a / b d / ( 2 cos2 P) одновременно представляет собой радиус делительной окружности эквивалентного прямозубого цилиндрического колеса. [1]
Теперь нужно найти радиус кривизны эллипса в точке А. [2]
Окружность 2 - крайняя правая; радиус ее является радиусом кривизны огибающего эллипса в точке / 2, а вершина располагается в крайней правой точке ( точка С) участка ABC вспомогательного эллипса. Окружность 3 - средняя окружность, она имеет наибольший радиус и касается огибающего эллипса в наивысшей его точке - точке В, а вершина этой окружности располагается в наивысшей точке ( точка В) участка ABC вспомогательного эллипса. Наконец, окружность 4 - это окружность общего положения ( текущая окружность рассматриваемого семейства), она касается огибающего эллипса в точке М и имеет вершину в точке N, лежащей на участке ABC вспомогательного эллипса. Окружности общего расположения всплошную заполняют заштрихованную на рис. 5.32, г область. Каждой точке участка ABC вспомогательного эллипса соответствует определенное значение коэффициента иа, а следовательно, и определенный тип напряженного состояния. Точки F, и F % - точки пересечения вспомогательного эллипса с осью абсцисс - являются фокусами огибающего эллипса. [3]
Для определения условий зацепления шевера и колеса заменяем действительный шевер условным, с радиусом, равным радиусу кривизны эллипса в точке малой полуоси. Радиус условного шевера Qycjl определяем по приведенной формуле. Аналогично пересчитываем радиусы условных начальных окружностей нового и переточенного шевера. [4]
Для определения условий зацепления шевера и колеса заменяем действительный шевер условным, с радиусом, равным радиусу кривизны эллипса в точке малой полуоси. Радиус условного шевера дусл определяем по приведенной формуле. Аналогично пересчитываем радиусы условных начальных окружностей нового и переточенного шевера. [5]
Приведенное число зубьев zt есть то число зубьев, которое имеет фреза с радиусом Rt, соответствующим радиусу кривизны эллипса в направлении малой его оси. [6]
Приведенное число зубьев z - t есть то число зубьев, которое имеет фреза с радиусом R [ t соответствующим радиусу кривизны эллипса в направлении малой его оси. [7]
На рис. 5.32, в изображены оба эллипса и четыре окружности Мора из бесконечного множества окружностей семейства, соответствующего выбранной комбинации оокт и токт. Окружность / - крайняя левая; радиус ее является радиусом кривизны огибающего эллипса в точке / Сь а вершина располагается в крайней левой точке ( точка А) участка ABC вспомогательного эллипса. [8]
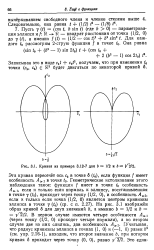 |
Кривая из примера - 7 для b 1 / 2 и b J / 2 / 2. [9] |
Геометрическое истолкование этого наблюдения такое: функция / имеет в точке t0 особенность A i, если и только если нормаль к эллипсу, восстановленная в точке у ( f0), проходит через точку ( 1 / 2, 0), и особенность Л2, если и только если точка ( 1 / 2, 0) является центром кривизны эллипса в точке v ( A) ( ср. На рис. 3.1 изображен образ кривой б для двух значений Ь, а именно b 1 / 2 и. Учитывая, что радиус кривизны эллипса в точках ( 1, 0) и ( - 1, 0) равен Ь2 ( см. упр. [10]
Исключение составляют, разумеется, те точки, где радиус кривизны имеет экстремальное значение. Так, вблизи вершины О, где радиус кривизны параболы имеет минимальное значение, парабола целиком лежит вне круга кривизны Ct. Напротив, вблизи вершины В, где радиус кривизны эллипса имеет максимальное значение, эллипс ( см. рис. 180) располагается целиком внутри соответствующего круга кривизны С. [11]
Страницы: 1