Радиус - рассеивающая масса
Cтраница 1
Радиус рассеивающей массы можно рассчитать из наклона этой прямой. До сих пор наиболее широко данные измерений рассеяния под малыми углами используются для такого расчета размера частицы из наклона прямой. Но, как будет показано в этом разделе, эта характеристика ни в коем случае не является единственным параметром, который можно получить из данных рассеяния под малыми углами. [1]
Радиус рассеивающей массы можно легко рассчитать для частиц, имеющих геометрически правильную форму. [2]
Отсюда видно, что не составляет особого труда подобрать частицы такой формы, для которых радиус рассеивающей массы и объем согласуются с экспериментально наблюдаемыми величинами, но такой метод, безусловно, неоднозначен. [3]
Точный расчет кривых рассеяния для частиц различной формы, а также многие экспериментальные данные показывают, что часто встречаются значительные отклонения формы кривых от гауссовой кривой. Тем не менее это не оказывает влияния на один очень важный результат теоретических выводов Гинье: тангенс угла наклона кривой при нулевом угле дает правильную величину радиуса рассеивающей массы. Если известен молекулярный вес и плотность вещества, можно рассчитать радиус рассеивающей массы, Rmm, который имели бы частицы, будь они сферическими. [4]
Точный расчет кривых рассеяния для частиц различной формы, а также многие экспериментальные данные показывают, что часто встречаются значительные отклонения формы кривых от гауссовой кривой. Тем не менее это не оказывает влияния на один очень важный результат теоретических выводов Гинье: тангенс угла наклона кривой при нулевом угле дает правильную величину радиуса рассеивающей массы. Если известен молекулярный вес и плотность вещества, можно рассчитать радиус рассеивающей массы, Rmm, который имели бы частицы, будь они сферическими. [5]
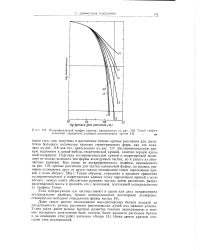 |
Логарифмический график кривых, приведенных на 118. Такой график позволяет определить размеры рассеивающих частиц.., -. [6] |
Экспериментальную кривую подгоняют к какой-нибудь теоретической кривой, сдвигая первую вдоль осей координат. Подгонка экспериментальной кривой к теоретической позволяет не только выяснить тип формы исследуемых частиц, но и узнать их абсолютные размеры. Таким образом, определив в процессе сравнения экспериментальной и теоретических кривых точку пересечения кривой с осью абсцисс, можно найти абсолютные размеры частиц, затем рассчитать радиус рассеивающей массы и сравнить его с величиной, полученной непосредственно из графика Гинье. [7]
Резко выраженная кривизна графика Гинье для кривой рассеяния от этого вещества указывает на анизотропную форму его молекул. Было высказано предположение, что исследуемые частицы имеют палочкообразную форму. Предположение основано на том, что зависимость интенсивности от угла рассеяния определяется двумя факторами. Первый связан с наличием очень длинных частиц, а другой зависит от радиуса инерции поперечного сечения, определяемого как среднеквадратичное расстояние электронов от оси вытянутой частицы. Наклон кривой в области очень малых углов говорит о том, что палочки не бесконечно длинные и имеют радиус рассеивающей массы 70 А; из второго наклона кривой получается радиус рассеивающей массы для поперечного сечения частиц, равный 15 А. [8]
Резко выраженная кривизна графика Гинье для кривой рассеяния от этого вещества указывает на анизотропную форму его молекул. Было высказано предположение, что исследуемые частицы имеют палочкообразную форму. Предположение основано на том, что зависимость интенсивности от угла рассеяния определяется двумя факторами. Первый связан с наличием очень длинных частиц, а другой зависит от радиуса инерции поперечного сечения, определяемого как среднеквадратичное расстояние электронов от оси вытянутой частицы. Наклон кривой в области очень малых углов говорит о том, что палочки не бесконечно длинные и имеют радиус рассеивающей массы 70 А; из второго наклона кривой получается радиус рассеивающей массы для поперечного сечения частиц, равный 15 А. [9]
Линейная зависимость указывает на то, что форма частиц заметно не отклоняется от сферической. На рис. 121 приведены кривые рассеяния, соответствующие растворам этого белка различной концентрации. Из этих кривых видно, что даже при очень низкой концентрации белка происходит интерференция лучей, рассеянных различными частицами; эти эффекты в значительной степени искажают рассеяние, свойственное самим частицам. Таким образом, измерения, результаты которых приведены на рис. 120, были выполнены с растворами слишком высокой концентрации. Тем не менее из каждой кривой можно получить кажущийся радиус рассеивающей массы. При сравнении логарифмического графика экстраполированной кривой рассеяния сывороточного альбумина, в которую внесена поправка на коллимацию, с теоретическими кривыми для эллипсоидов ( приведенными на рис. 1 19) оказывается, что радиус рассеивающей массы равен 29 8 А; частицы имеют форму сплющенных эллипсоидов с соотношением осей 3 5 и характеризуются внутренней гидратацией, причем на 1 г белка приходится 0 37 г воды. [10]
Точный расчет кривых рассеяния для частиц различной формы, а также многие экспериментальные данные показывают, что часто встречаются значительные отклонения формы кривых от гауссовой кривой. Тем не менее это не оказывает влияния на один очень важный результат теоретических выводов Гинье: тангенс угла наклона кривой при нулевом угле дает правильную величину радиуса рассеивающей массы. Если известен молекулярный вес и плотность вещества, можно рассчитать радиус рассеивающей массы, Rmm, который имели бы частицы, будь они сферическими. С помощью этого фактора анизотропии ( f), специфичного для самой частицы, отношение вязкостей, полученное из данных ультрацентрифугирования, можно разделить на два компонента: первый - связанный с сольватацией и второй - характеризующий анизотропию частицы. Если имеет место внутренняя сольватация частицы ( встречающаяся у белков), то величина /, полученная из данных рассеяния под малыми углами, определяется как внутренним набуханием ( которое приводит к увеличению радиуса рассеивающей массы), так и анизотропией частицы. Поскольку объем частицы можно оценить прямым независимым методом ( это будет показано ниже), то, сравнив полученный объем с молекулярным весом частицы, можно определить, имеет ли место на самом деле внутреннее набухание. Таким образом, становится возможным выделить тот компонент, который обусловлен исключительно формой частицы. [11]
Для нахождения этого параметра существует несколько способов. Для начала следует отметить, что рассеяние от плотно упакованных систем при очень малых углах можно приблизительно описать уравнением, аналогичным приближенному выражению, предложенному Гинье для описания рассеяния от отдельных частиц. В этом случае, как правило, нельзя получить гауссову кривую, но по крайней мере удовлетворительное соответствие должно иметь место. С математической точки зрения это сходство с гауссовой кривой объясняется тем, что кривая рассеяния, если ее изобразить в виде степенного ряда, всегда описывается четной функцией. Этот параметр можно представить как радиус рассеивающей массы сферической частицы, заменяющей реальное рассматриваемое тело, для которой электронная плотность дается корреляционной функцией. [12]
Страницы: 1