Радиус - мембрана
Cтраница 1
Радиус мембраны вьи-бирается по конструктивным. [1]
Зависимость коэфициента активности мембраны ам от ее конструкции и установки: г - радиус обжимных дисков; R - радиус мембраны; 1 - плоская мембрана без дисков; 2 - плоская мембрана с дисками; 3 - мембрана с канавкой и дисками; 4 - трапецеидальная мембрана с дисками; 5 - гармоникообразиая мембрана. [2]
Др - разность давлений; Е - модуль упругости материала мембраны; Д - толщина материала мембраны; R - радиус мембраны; А и В - коэффициенты, зависящие от формы гофра; h - прогиб центра мембраны. [3]
Очевидно, р c / sin а, или, вследствие малости &, р а / а, где а - радиус мембраны. [4]
Очевидно, р a / sin а, или, вследствие малости а, р и а / а, где а - радиус мембраны. [5]
Очевидно, p - a / sin a, или, вследствие малости а, р а / а, где а - радиус мембраны. [6]
Следует отметить, что при таком методе расчета ограничивается только одно главное напряжение ( радиальное), которое является наибольшим во всех точках радиуса мембраны, кроме центра, где оно равно другому главному напряжению. Влияние второго главного напряжения ( в окружном направлении) на усталостную прочность мембраны учитывается при выборе коэффициента запаса. [7]
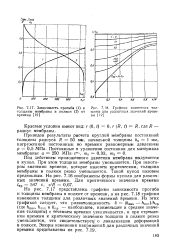 |
Зависимость прогиба ( / и толщины мембраны в полюсе ( 2 от времени.| Графики изменения толщины для различных значений времени. [8] |
Краевые условия имеют вид: г ( 0, t) 0, г ( R, t) R, где R - радиус мембраны. [9]
Для того, чтобы при свободно опертой по краю мембране ( например, в случае б) получить частоту свободных колебаний порядка 1000 гц, необходимо уменьшить радиус мембраны или увеличить ее толщину. [10]
Расчет гофрированных металлических мембран значительно сложнее. Кроме толщины и радиусов мембраны на ее характеристику существенно влияют число, форма и размеры как основных, так и краевого гофров. Для упрощения расчетов используют номограммы, приведенные в специальной литературе. [11]
Исследования манометра, проведенные во ВНИИМ, показали, что погрешности измерения давления, зависящие от диэлектрической проницаемости, от температуры ( в случае термостатировання корпуса манометра) и от газовой десорбции, на рабочих поверхностях могут считаться пренебрежимо малыми. Основными являются погрешность определения емкости и радиусов мембраны и электрода, входящих в уравнение постоянной, аналогичное выражению (1.62), а также погрешность измерения компенсирующего напряжения. [12]
 |
Основные характеристики преобразователей силы. [13] |
Заданную собственную частоту обеспечивают соответствующим выбо - ром радиуса мембраны. [14]
У & г. Однако здесь уже необходимо учитывать граничные условия. Предположим, в частности, что мембрана закреплена по краю, так что для всех граничных точек / ( р) 0, где р - радиус мембраны. Чтобы удовлетворить граничным условиям, аргумент функции Бесселя при: г-р должен совпадать с одним из этих нулей. [15]
Страницы: 1 2