Радиус - окружность
Cтраница 1
Радиусы окружности проектируются на два ее взаимно перпендикулярных диаметра и на проекциях, как на полуосях, строятся эллипсы. [1]
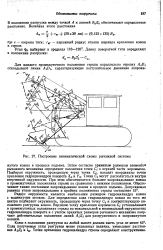 |
Построение кинематической схемы рычажной системы. [2] |
Радиус окружности является наибольшим размером гидроцилиндра ковша с выдвинутым штоком. Для определения хода гидроцилиндра ковша из того же центра подбирают окружность, проходящую через точку Съ и соответствующую положению разгрузки ковша. [3]
Радиус окружности, на периферии которой пропускание света уменьшается на 60 % по сравнению с центром поля. [4]
 |
Определение удельного заряда Э - частиц. [5] |
Радиус окружности г можно определить, измеряя смещение пучка z - на фотопластинке и зная расстояние ] от края конденсатора до пластинки. [6]
 |
Расположение ионов в слое, образованном гранями кубов в кристалле галогенида щелочного металла со структурой хлористого натрия. [7] |
Радиусы окружностей на этом рисунке соответствуют кристаллическим радиусам ионов. [8]
Радиус окружностей, описываемых лучом в плоскости изображения, будет пропорционален 3 - й степени апертурного угла. Картина волновой и поперечной аберраций показана на фиг. [9]
Радиус окружности равен нулю. Эта точка лежит на параболе. Значит, уравнение действительных корней не имеет. [10]
 |
Плоскости ножей. [11] |
Радиус окружности, образуемой режущими гранями ножей, должен быть меньше наружного радиуса перерубаемой трубы. Угол заострения ножей 60, Процесс рубки состоит в следующем. При сближении ножи в первый момент касаются трубы в восьми точках. При дальнейшем сближении они врезаются в трубу, при этом образуются лунки, располагаемые по окружности. [12]
Радиус окружности равен расстоянию ее центра от касательной. Прямые 1) и 2) пересекают окружность; прямая 3) касается и 4) проходит вне окружности. О расположении прямых относительно окружности мы судим по расстоянию этих прямых от центра. В зависимости от того, будет ли это расстояние меньше, равно или больше радиуса - прямая пересекает, касается или проходит вне окружности. Радиус, проходящий через данную точку, перпендикулярен к искомой хорде. [13]
Радиус окружности равен расстоянию ее центра от касательной. J - 3; - 1) и ( - ] - 2; - 2); 2) прямая касается окружности в точке ( - 4; 6); 3) действительных точек пересечения нет. Прямые 1) и 2) пересекают окружность; прямая 3) касается и 4) проходит вне окружности. О расположении прямых относительно окружности мы судим по расстоянию этих прямых от центра. В зависимости от того, будет ли это расстояние меньше, равно или больше радиуса - прямая пересекает, касается или проходит вне окружности. Радиус, проходящий через данную точку, перпендикулярен к искомой хорде. [14]
 |
Конформное отображение малой окрестности точки заострении крылового профиля и выбор циркуляции по постулату Жуковского-Чаплыгина. [15] |
Страницы: 1 2 3 4