Радиус - производящая окружность
Cтраница 1
Радиус производящей окружности для эпициклоидальных участков PiDj и Р В и удлиненно-эпициклоидальных участков В С и BiCi rpll 66 мм. [1]
 |
Построение касательной к эпициклоиде. [2] |
Воспользовавшись радиусом производящей окружности R ОС и линией центров этих окружностей, находим центр окружности, когда на ней находится точка Р, - точку Ог Соединив точку О, с центром О2, получим точку М производящей окружности в рассматриваемом положении. [3]
Если для сопряженных колес, заданных центроидами, радиус внутренней производящей окружности гх принять равным эксцентриситету h, а радиус второй производящей окружности - равным нулю, получим центроидное гипо-циклоидальное зацепление. [4]
Во избежание ослабления зуба циклоидального зацепления у основания ножки радиусы производящих окружностей обычно принимают равными 0 4 - 0 3 радиуса той начальной - окружности, внутри которой располагается производящая окружность. [5]
Во избежание ослабления зуба циклоидального зацепления у основания ножки радиусы производящих окружностей обычно принимают равными 0 4 - 0 3 радиуса той начальной окружности, внутри которой располагается производящая окружность. [6]
Принимая эти точки пересечения за центры, описывают из них дуги радиусом производящей окружности до пересечения их с соответствующими им дугами, проведенными из центра О. Полученные в пересечении их точки соединяют при помощи лекала плавной кривой. [7]
 |
Общий случай движения электрона во взаимно перпендикулярных однородных электрическом и магнитном полях ( § L8. [8] |
Трохоидальное движение совершает точка на спице колеса, катящегося вдоль оси, причем радиус производящей окружности, точка кото - Рой описывает трохоиду, в общем СЛуЧае не равен радиусу катящейся окружности. [9]
Здесь верхние знаки относятся к эпициклоиде, нижние - к гипоциклоиде, г - радиус производящей окружности, R - радиус центроиды, г - переменный параметр. [10]
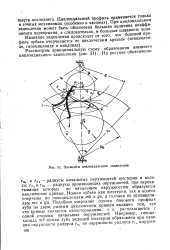 |
Элементы циклоидального зацепления. [11] |
Гн, и /, - радиусы начальных окружностей шестерни и колеса; rnt и гп, - радиусы производящих окружностей, при перекатывании которых по начальным окружностям образуются циклические кривые. [12]
Гипоциклоида обращается в радиальную прямую, если диаметр производящей окружности принять равным радиусу начальной, и обращается в точку, если радиус производящей окружности равен нулю или радиусу начальной окружности. [13]
Осью тора является координатная ось у; радиус ( расстояние от центра производящей окружности до оси вращения) осевой линии тора 60 мм, а радиус производящей окружности Ri. [14]
При удлиненно-циклоидальном профилировании на нагнетании появляется защемленный объем. Величина его возрастает с увеличением радиуса гй производящей окружности. [15]
Страницы: 1 2