Радиус - полость
Cтраница 2
Катион является плоским; длина связи определена по радиусу квазнцилиидрнческой полости в предположении, что длины всех связей С-С равны. [16]
Используя уже приводившееся значение энергии оптического перехода, определяем радиус полости, который оказывается равным - 3 3 А. [17]
Таким образом, длина свободного пробега оказывается почти равной радиусу полости. Это равенство легко может быть заменено нужным нам неравенством ери помощи незначительного изменения исходных цифр в пределах экспериментальных условий. [18]
Пусть ось цилиндрической полости совпадает с осью г, а радиус полости равен а. Продольная волна распространяется параллельно оси г с фазовой скоростью с. Предположим, что волна характеризуется осевой симметрией относительно оси г. Эту осе-симметричную задачу наиболее удобно решать с использованием потенциалов. [19]
Радиус поверхности раздела областей упругого и пластического деформирования массива; R - радиус полости; Р - давление, приложенное к внутренней поверхности полости. [20]
Анализ этого выражения показывает, что скорость движения границы нарастает по мере уменьшения радиуса полости. [21]
Для значений электронной плотности р, равных числу валентных электронов в единице объема полимера, радиус полостей меняется от 3 1 до 4 1 А, а Л / Эф составляет примерно 0 5 - Ю19 - - 1 3 - 1019 см - для разных композиций. [22]
Для значений электронной плотности р, равных числу валентных электронов в единице объема полимера, радиус полостей меняется от 3 1 до 4 1 А, а Л / эф составляет примерно 0 5 - 1019 - - 1 3 - 1019 см - для разных композиций. [23]
Условие ( 2) требует равенства - - 0 при г а, где а - радиус полости. [24]
Таким образом, используя формулы для перемещений и скоростей, а также формулу (2.1.3), находим радиус полости гпол как функцию времени. [25]
Таким образом, используя формулы для перемещений и скоростей, а также формулу (2.1.3), находим радиус полости гаол как функцию времени. [26]
Здесь г2 х2 У2 & х, у, z - декартовы координаты ( рис. 38); радиус шаровой полости а принят за единицу длины. [27]
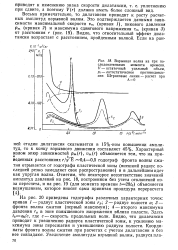 |
Взрывная волна на три последовательных момента времени. V-остаточный удельный объем, Pi - литостатическое противодавле. [28] |
На рис. 20 приведены годографы различных характерных точек: кривая 1 - радиус пластической зоны гр; 2 - радиус полости а; 3 - фронта волны сжатия ( первый максимум); 4 - второго максимума давления га в зоне повышенного напряжения вблизи полости. [29]
Еще одна проблема возникает при введении в матричные элементы Хартри - Фока той составляющей электронной плотности, которая лежит вне радиуса полости; это противоречит принятому в данной модели предположению, согласно которому молекула должна быть расположена внутри полости. Однако найдено, что вклад электронной плотности вне полости в ( 8 - 32) незначителен. [30]
Страницы: 1 2 3 4