Радиус - поперечное сечение
Cтраница 2
В сечениях тонкостенной трубы с радиусом поперечного сечения R и толщиной стенки 5 действуют растягивающая сила Р и крутящий момент М PR. Труба изготовлена из листа двумя способами: 1 - края листа сварены, 2 - края листа свободны. [16]
Пусть круговой цилиндр длиной /, радиусом поперечного сечения г, защемленный левым концом, подвергается на правом свободном конце действию пары сил, лежащей в плоскости сечения; момент этой пары равен Мх. [17]
Формула (2.24) устанавливает линейную зависимость касательного напряжения вдоль любого радиуса поперечного сечения. [18]
Известно, что для тороидального образца с радиусом поперечного сечения, существенно меньшим радиуса тора, и намагничивающей обмоткой, намотанной равномерно по всей длине тора, коэффициент размагничивания равен нулю. [19]
Как было показано выше, теоретически зависимость изменения радиуса поперечного сечения факела по его длине является прямо пропорциональной. Эта же зависимость подтверждается экспериментом. [20]
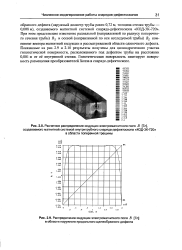
При этом представлено изменение радиальной ( направленной по радиусу поперечного сечения трубы) Вх и осевой ( направленной по оси исследуемой трубы) В2 компонент вектора магнитной индукции в рассматриваемой области одиночного дефекта. Показанные на рис. 2.9 и 2.10 результаты получены для цилиндрического участка гипотетической поверхности, расположенного под дефектом трубы на расстоянии 0 001 м от ее внутренней стенки. Гипотетическая поверхность имитирует поверхность размещения преобразователей Холла в снаряде-дефектоскопе. [22]
На рисунке 105 изображен полый цилиндрический проводник с радиусами поперечного сечения Л и г. Текущий по проводу ток i равномерно распределен по его поперечному сечению. [23]
Пуассона, Ei - модуль упругости, п - радиус поперечного сечения соударяющихся стержней. [24]
Вспоминая, что функция F ( x) пропорциональна радиусу поперечного сечения, видим, что уравнение (4.5.3.18) является уравнением одномерной теплопроводности. Оно возникло здесь как формальное следствие граничного условия на теплоизолированной боковой поверхности. Для равномерной точности этого приближения в центральном сечении стержня функция F ( x) должна быть достаточно гладкой. [25]
В - аберрационная постоянная; га - радиус диафрагмы или радиус поперечного сечения пучка внутри линзы. [27]
Допустимость последнего упрощения обусловлена малостью толщины ламинарного подслоя по сравнению с радиусом поперечного сечения цилиндра. Поэтому формула ( 37) по существу дает величину цл для пластин. [28]
Предполагается, конечно, что ось цилиндра пересекает поверхность шара и что радиус поперечного сечения цилиндра меньше радиуса шара. [29]
Во-вторых, изнашивающий поверхность цилиндр предлагается таких размеров, для которых разность радиусов поперечных сечений мала. [30]
Страницы: 1 2 3 4