Первый боровский радиус

Cтраница 2

При 81 и т т эти уравнения относятся к атому водорода, для которого энергия ионизации основного состояния 13 6 эв, а радиус наименьшей орбиты / 0 528 А. В случае германия, для которого е16, а т п 1ljn, из (13.4.7) и (13.4.3) следует, что энергия ионизации основного состояния донора приблизительно в 1000 раз меньше, а первый боровский радиус приблизительно в 64 раза больше. Если бы оказалось иначе, возникли бы серьезные сомнения относительно правомерности такой модели. Поскольку энергия ионизации при обычных температурах много меньше kT, то при нормальных условиях донорные уровни будут почти полностью ионизованы. Таким образом, полученные величины удовлетворительно согласуются с оценками энергии ионизации донора, полученными из измерений инфракрасного поглощения и низкотемпературной проводимости. [16]

При е 1 и т т эти уравнения относятся к атому водорода, для которого энергия ионизации основного состояния 6 13 6 эв, а радиус наименьшей орбиты 0 528 А. В случае германия, для которого е - 16, а т; 1 / im, из (13.4.7) и (13.4.3) следует, что энергия ионизации основного состояния донора приблизительно в 1000 раз меньше, а первый боровский радиус приблизительно в 64 раза больше. Если бы оказалось иначе, возникли бы серьезные сомнения относительно правомерности такой модели. Поскольку энергия ионизации при обычных температурах много меньше kT, то при нормальных условиях донорные уровни будут почти полностью ионизованы. Таким образом, полученные величины удовлетворительно согласуются с оценками энергии ионизации донора, полученными из измерений инфракрасного поглощения и низкотемпературной проводимости. [17]

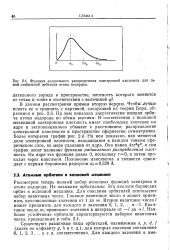Функция радиального распределения электронной плотности для самой стабильной орбитами атома водорода. [18]

Чтобъ Лучше понять ее и сравнить с картиной, следующей из теории Бора, обратимся к рис. 2.3. На нем показана энергетически низшая орбита атома водорода по обеим версиям. В соответствии с волновой механикой электронная плотность имеет наибольшее значение на ядре и экспоненциально убывает с расстоянием; распределение электронной плостности в пространстве сферически симметрично. Более интересен график рис. 2.4. На нем показано, как меняется доля электронной плотности, находящаяся в каждом тонком сферическом слое, по мере удаления от ядра. Она равна 4яг2о А а сам график носит название функции радиального распределения плот ности. На ядре эта функция равна 0, поскольку г0, а затем проходит через максимум. Положение максимума в точности совпадает с первым боровским радиусом а00 529 А. [19]

Страницы: 1 2