Наружный радиус - диск
Cтраница 1
Наружный радиус диска определяем по (1.52): RV ( 115 0, 5 - 23 0, 25 - 182 116 мм. [1]
Так как наружный радиус диска принимают по основанию впадин замков, то замочные части лопатки и диска считают продолжением профильной части лопатки. При большом числе лопаток можно считать, что они вызывают равномерно распределенные нагрузки на ободе диска. [2]
Граничное условие на наружном радиусе диска одинаково для ди-сков с центральным отверстием и для сплошных дисков. Второе граничное условие существенно связано с наличием или отсутствием центрального отверстия. [3]
Здесь через Ъ обозначен наружный радиус диска. [4]
Так, переходя от ступени к ступени, выясняются предварительные напряжения на наружном радиусе диска. [5]
R - независимые переменные, означающие радиальное расстояние, в см; Ъ - наружный радиус диска в см; а - радиус центрального отверстия в см; h - толщина диска на радиусе г в см; Т - температура диска на радиусе г в С; аг - радиальное напряжение в кГ см; ot - окружное напряжение в кГ см агь - радиальное напряжение на радиусе Ь, вызванное силами инерции лопаток и замков, в лгГ / c - W2; оа - радиальное напряжение на радиусе а; апр-приведенное напряжение в кГ / сл2 ( см. гл. [6]
При выводе дифференциального уравнения, описывающего напряженное состояние тонкого диска, приняты следующие предположения: осевой размер диска значительно меньше наружного радиуса диска, напряжения в диске равномерно распределены по его толщине, деформации вдоль оси диска достаточно малы и ими можно пренебречь, температура диска не меняется по толщине, а изменяется только по радиусу. [7]
Характеристики модели: внутренний радиус диска ( R) - 0 0508 м; толщина диска - 0 00635 м; наружный радиус диска ( г) - 0 18034 м; радиус конца лопатки ( Ь) - 0 24638 м; ширина лопатки - 0 031475 м; толщина лопатки - 0 003175 м; длина лопатки ( а) - 0 06604 м, угол сектора - 30; частота вращения - 10000 об / мин; материал - сталь. [8]
В этом расчете приняты следующие обозначения: р-плотность материала диска в кГ - сенР / см; Е - модуль упругости материала в кГ смг а - коэффициент линейного расширения материала; ft - коэффициент Пуассона, здесь принято р 0 5; ш - угловая скорость вращения диска в рад / сек; г, R - независимые переменные, означающие радиальное расстояние, в см; Ь - наружный радиус диска в см; а - радиус центрального отверстия в см; h - толщина диска на радиусе г в см; Т - температура диска на радиусе г в С; ог - радиальное напряжение в кГ / см2; at - окружное напряжение в кГ / см2; агь - радиальное напряжение на радиусе Ъ, вызванное силами инерции лопаток и замков, в лгГ / еж; ага - радиальное напряжение на радиусе а; пр - приведенное напряжение в кГ / см ( см. гл. [9]
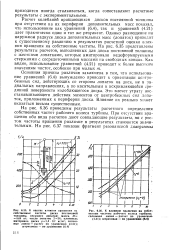
Расчет колебаний вращающихся дисков постоянной толщины при отсутствии на их периферии дополнительных масс показал, что использование как уравнений (6.4), так и уравнений (4.21) дает практически один и тот же результат. Однако размещение на наружном радиусе диска дополнительных масс ( лопаток) приводит к существенному различию в результатах расчетной оценки влияния вращения на собственные частоты. На рис. 6.35 представлены результаты расчетов, выполненных для диска постоянной толшины с жесткими лопатками, которые имитировали недеформируемыми стержнями с сосредоточенными массами на свободных концах. [11]
 |
Графики для построения профиля кольца по его радиальному размеру. [12] |
Радиальные напряжения в равнопрочной части диска нарастают к периферии. Для удовлетворения граничным условиям на наружном радиусе диска, где радиальное напряжение равно нулю, иногда приходится выполнять бурт со ступенчатым переходом к нему от минимальной толщины hr равнопрочной части. [13]
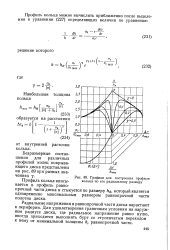 |
Графики для построения профиля кольца по его радиальному размеру. [14] |
Радиальные напряжения в равнопрочной части диска нарастают к периферии. Для удовлетворения граничным условиям на наружном радиусе диска, где радиальное напряжение равно нулю, иногда приходится выполнять бурт со ступенчатым переходом к нему от минимальной толщины Нг равнопрочной части. [15]
Страницы: 1 2