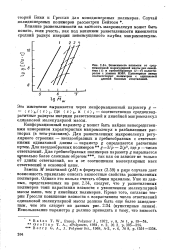
Среднеквадратичный радиус

Cтраница 3

СГС) или квадратных метрах ( СИ), где я2 - среднеквадратичный радиус инерции невозмущенной цепи, а - параметр набухания. [31]

По упругому рассеянию электронов были также измерены формфак-торы, а соответственно, и среднеквадратичные радиусы заряженных тг-и Jf-мезонов. Однако в этом случае постановку эксперимента пришлось обратить: поскольку пионы и каоны не могут быть использованы в качестве мишеней, их пучки рассеивали на электронах в атоме, которые в данном случае можно считать свободными. Установки регистрировали как рассеявшиеся тг ( или) - мезоны, так и выбитые из атома электроны. Отбирались события, соответствующие кинематике упругого рассеяния пионов ( или каонов) заданной энергии на электронах. [32]

Несмотря на то, что соотношение ( 15) было получено при сравнении среднеквадратичных радиусов вращения совершенной звезды и линейной макромолекулы, оно с достаточной для практических целей точностью удовлетворяет реальным зависимостям для разветвленных макромолекул. Анализ данных Шафгена и Флори 61 для линейного и разветвленного полиамидов и данных Турмонда и Зимма 66 для разветвленного полистирола на основании формулы ( 15) позволяет судить об обоснованности сделанного предположения. [33]

Несмотря на то, что соотношение ( 15) было получено при сравнении среднеквадратичных радиусов вращения совершенной звезды и линейной макромолекулы, оно с достаточной для практических целей точностью удовлетворяет реальным зависимостям для разветвленных макромолекул. Анализ данных Шафгена и Флори61 для линейного и разветвленного полиамидов и данных Турмонда и Зимма66 для разветвленного полистирола на основании формулы ( 15) позволяет судить об обоснованности сделанного предположения. [34]

Несмотря на то, что соотношение ( 15) было получено при сравнении среднеквадратичных радиусов вращения совершенной звезды и линейной макромолекулы, оно с достаточной для практических целей точностью удовлетворяет реальным зависимостям для разветвленных макромолекул. Анализ данных Шафгена и Флори 61 для линейного и разветвленного полиамидов и данных Турмонда и Зимма66 для разветвленного полистирола на основании формулы ( 15) позволяет судить об обоснованности сделанного предположения. [35]

Использовалось два типа аэрозолей: монодисперсный со среднеквадратичным радиусом 2 6 мкм и полидисперсный со среднеквадратичным радиусом 2 9 мкм. [36]

Выше уже указывалось, что степень разветвленное полимерных молекул можно оценивать по величине g, равной отношению среднеквадратичных радиусов инерции разветвленной и неразветвленной цепей, содержащих одинаковое число сегментов, причем значение g с возрастанием степени разветвленности уменьшается. Тогда, естественно, можно ожидать, что с увеличением степени разветвленности будет уменьшаться и характеристическая вязкость, которая пропорциональна T-O S / I. [37]

Выше уже указывалось, что степень разветвленности полимерных молекул можно оценивать по величине g, равной отношению среднеквадратичных радиусов инерции разветвленной и неразветвленной цепей, содержащих одинаковое число сегментов, причем значение g с возрастанием степени разветвленности уменьшается. Тогда, естественно, можно ожидать, что с увеличением степени разветвленности будет уменьшаться и характеристическая вязкость, которая пропорциональна ( Оо / 2 - Это явление наблюдали Краус и Грювер 83 для разветвленных полибутадиенов, полученных на к-бутиллитии. [38]

Распределение плотности заряда и магнитного момента в протоне и магнитного момента в нейтроне носит экспоненциальный характер со среднеквадратичным радиусом 0 8 ферми. Результаты, относящиеся к распределению заряда в нейтроне, менее однозначны. Таким образом, от старых результатов сохранились только значения среднеквадратичных радиусов, но зато были получены новые, очень интересные результаты. [39]

Зависимость вязкости от сред-немассовой молекулярной массы для линейных ( / и гребнеобразных ( 2 - 4 полиств-ролов с узкими ММР. Пунктирные линии соответствуют полимерам с одинаковой длиной боковых ответвлений. [40]

Это изменение выражается через конформационный параметр g ( s brl ( s, где ( s У Ьг и s, - соответственно среднеквадратичные радиусы инерции разветвленной и линейной макромолекул одинаковой молекулярной массы. [41]

Наиболее часто экспериментально определяют ( / г2) 1 / 2 - среднеквадратичное расстояние между концами цепи и ( Rz) / г - среднеквадратичный радиус инерции. Эти величины определяют гидродинамические, реологические и многие другие свойства растворов и расплавов полимеров. [42]

Марка-Хоувинка; К, К - коэффициенты в уравнении Марка-Хоувинка; я - коэффициент расширения ( или фактор вытягивания) молекулярного клубка; ( s2) - среднеквадратичный радиус инерции. [43]

Определив а, по уравнению ( 4) рассчитывают величину Ф, а затем по формулам ( 2) и ( 3) - среднеквадратичное расстояние между концами цепи и среднеквадратичный радиус инерции. [44]

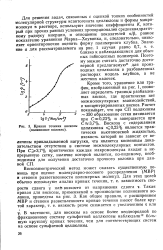Кривая течения вискозы nmn. [45]

Страницы: 1 2 3 4