Эквивалентный радиус - частица
Cтраница 1
Средневесовой эквивалентный радиус частиц г может быть вычислен по формуле ( см. введение к гл. [1]
Средневесовой эквивалентный радиус частиц rv может быть вычислен по формуле ( см. введение к гл. [2]
Расчет эквивалентных радиусов частиц проводят но уравнению ( V. Расчет по номограмме ведут в следующем порядке. [3]
По данной кривой находится эквивалентный радиус частиц, соответствующий относительному суммарному содержанию более мелких частиц, равному допускаемому в фугате содержанию твердой фазы, отнесенному к содержанию последней в суспензии. [4]
По уравнению ( 4) вычисляют эквивалентные радиусы частиц, полностью осевших к моментам времени, соответствующим построенным ординатам. [5]
Определив экспериментально эти величины и рассчитав константу К, можно вычислить эквивалентные радиусы частиц, оседающих за те или иные промежутки времени. [6]
Определив эти величины экспериментально и рассчитав константу Стокса, можно вычислить эквивалентные радиусы частиц, оседающих за определенные промежутки времени. [7]
Определив экспериментально эти величины и рассчитав константу К, можно вычислить эквивалентные радиусы частиц, оседающих за те или иные промежутки времени. [8]
Определив экспериментально эти величины и рассчитав константу / С, можно вычислить эквивалентные радиусы частиц, оседающих за те или иные промежутки времени. [9]
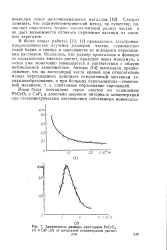 |
Зависимость размера кристаллов РЬСгО4 ( / и CaF2 ( 2 от начальной концентрации растворов. [10] |
Следует заметить, что седиментометрический метод, по существу, позволяет определять только эквивалентный радиус частиц и не дает возможности отличать первичные частицы от сложных агрегатов. [11]
 |
К расчету. [12] |
Уравнение (V.18) и рис. V.4 в дополнение к сказанному выше обосновывают определение эквивалентных радиусов частиц методом графической обработки седиментационной кривой: отрезок ординаты mi, отсекаемый касательной, дает массу седиментационного осадка, содержащего все частицы с г rt, a радиус Г [ частиц, рассчитанный для этого времени по уравнению (V.17), соответствует минимальному радиусу тех частиц, которые полностью осели к этому времени. [13]
К числу основных характеристик дисперсной системы относятся, в частности, размер частиц наивероятнейшей фракции, средневе-совой эквивалентный радиус частиц и удельная поверхность суспензии. [14]
Влияние соотношения расхода масс на величину коэффициента массоотдачи на начальной стадии процесса показано на рис. 7.21. Зависимость коэффициента массоотдачи от размера частиц в фазе перехода от начальной стадии процесса к основной, где коэффициент массоотдачи неограниченно возрастает, показана на рис. 7.22. С увеличением эквивалентного радиуса частиц возрастает и коэффициент массоотдачи. [15]
Страницы: 1 2