Критический радиус - капля
Cтраница 1
Критический радиус капли прямо пропорционален коэффициенту поверхностного натяжения и обратно пропорционален пересыщению АР; чем более пересыщен пар, тем более мелкие капли способны служить зародышами жидкой фазы. [1]
Вычислим критический радиус капли для наступления конденсации пара. [2]
Нахождению зависимости критического радиуса капли при дроблении от различных характеристик сплошной и дисперсной фаз посвящено большое число работ. Приведем основные из полученных в них результатов. [3]
Таким образом отношение критического радиуса капли к диаметру d трубы зависит от двух безразмерных параметров We и РГ / РЖ. [4]
Следовательно, в рассматриваемом случае критический радиус капли имеет порядок Rcr - 100 мкм. [5]
Если переохлаждение невелико, то критический радиус капли, определяемый формулой (6.18), велик, и требуется очень большая флуктуация плотности, чтобы конденсация началась. При дальнейшем же увеличении давления или понижении температуры величина критического радиуса уменьшается. Поэтому вероятность соответствующей флуктуации увеличивается. [6]
Эта зависимость аналогична зависимости (12.39), приведенной выше для критического радиуса капли при конденсации пара. [7]
Из ( 34а) следует, что электрический заряд приводит к уменьшению критического радиуса капли при данной степени пересыщения пара. Этим объясняется качественным образом тот факт, что конденсация пара облегчается при наличия ионов. [8]
Из ( 34а) следует, что электрический заряд приводит к уменьшению критического радиуса капли при данной степени пересыщения пара. Этим объясняется качественным образом тот факт, что конденсация пара облегчается при наличия ионов. [9]
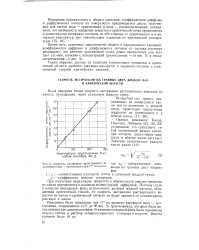 |
Скорость экстракции триэтиламина из где 312 - поверхностное натя-растворов вода - триэтиламин при 17 толуолом жение на границе двух жидких. [10] |
Однако измерения Бонда, Ньютона, Лебедева [21, 22, 23] установили, что существует такой критический радиус капли, при котором циркуляция жидкости в объеме капли затухает. [11]
Эта зависимость аналогична зависимости ( 12 - 39), приведенной выше для критического радиуса капли. [12]
Эта зависимость аналогична зависимости ( 12 - 36), приведенной выше для критического радиуса капли. [13]
Первая модель рассматривает распространение непрерывного излучения или длинного импульса СО2 - лазера с интенсивностью 104 - 105 Вт-см - 2 [1, 10, 23, 36] в капельных средах при широкой вариации размеров частиц. Существенной стороной модели является представление о пороге взрыва капель. Здесь порог взрыва определен по мгновенной интенсивности. В модели вводится понятие критического радиуса капли акр такого, что капли с а акр не разрушаются, а капли с аакр взрываются. [14]
Страницы: 1