Средний радиус - инерция
Cтраница 1
 |
Физические свойства олиго - и полиизобутиленов. [1] |
Средний радиус инерции sf 1 / 2 полиизобутилена в блоке 7 5 0 5нм и-7 7 0 5 нм в 0-растворителе. [2]
Можно ожидать, что средний радиус инерции макромолекул такого полимера в незаряженном состоянии RG будет равен приблизительно 150 А ( точная величина RG зависит, конечно, от природы полимера), но из табл. 33 видно, что при таких размерах макромолекулы наличие зарядов приводит к недопустимо высоким значениям свободной энергии. При относительно высокой ионной силе We ] заметно понижается уже при умеренном разворачивании молекул, и можно ожидать, что средняя кон-формация продолжает оставаться сферически симметричной, но молекула имеет увеличенный радиус инерции. Однако при низкой ионной силе необходимо значительно большее разворачивание молекулы. Модель Германса-Овербика, использованная при вычислении этих данных, конечно, является сверхупрощенной, и к приведенным значениям следует относиться не более как к полуколичественным результатам. Однако любая другая теория предсказывает в основном те же результаты, а именно, что ион полиэлектролита должен быть более развернут, чем соответствующая незаряженная макромолекула полимера, от которой он произошел. Все экспериментальные данные подтверждают это предположение. [3]
 |
Частные коэффициенты корреляции. [4] |
В настоящем разделе приводятся результаты исследования средних радиусов инерции дисперсных частиц и распределения их по размерам в описанных выше образцах. [5]
Па рис. 4.4 [6] изображены результаты измерения среднего радиуса инерции ( И2) 1 для клубков полистирола с М - 2 5 106, растворенного в декалине, от Т 31 С ( 0-точка) до Т - 120 С. Наличие второго участка увеличения размеров при изменении температуры от 90 до 120 С объяснить довольно трудно. [6]
Корень квадратный из этой величины носит название среднего радиуса инерции или радиуса эквивалентной сферы. Для гауссовых цепей справедливо. [7]
Влияние разветвленности на вязкость макромолекул может быть понято, если учесть, как под влиянием разветвленности изменяется средний радиус инерции невозмущенного клубка макромолекулы. [9]
Для описания пространственного расположения гибкой молекулы обычно используются два средних размера: среднее расстояние между концами цепи и средний радиус инерции. [10]
Степень свернутости полимерных цепей может быть охарактеризована несколькими величинами, а именно, средним расстоянием между концами цепи и средним радиусом инерции. [12]
Согласно Бюхе [89], физический смысл такой закономерности состоит в том, что гидродинамические размеры разветвленных клубков определяются не их средним радиусом инерции ( А. [13]
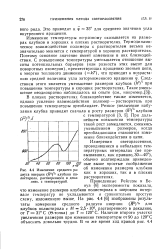 |
Изменение среднего радиуса инерции ( R2 / 2 клубков полистирола, растворенного в декалине, с температурой. [14] |
Проведенные Рейссом и Бе-нуа [6] эксперименты показали, что изменение размеров клубков полистирола в широком интервале температур не укладывается в сравнительно простую схему, изложенную выше. На рис. 4.4 [6] изображены результаты измерения среднего радиуса инерции ( Й2) / г для клубков полистирола с М 2 5 106, растворенного в декалине, от Т 31 С ( 6-точка) до Т 120 С. Наличие второго участка увеличения размеров при изменении температуры от 90 до 120 С объяснить довольно трудно. [15]
Страницы: 1 2