Радиус-вектор

Cтраница 3

Радиус-вектор ( линия, соединяющая Солнце и планету) описывает за равные промежутки времени равные площади. [31]

Радиус-вектор г из начала в переменную точку пространства М характеризуется криволинейными координатами qlt qt, q3 этой точки. [32]

Радиус-вектор, по определению, исходит из начала координат. Другие векторы имеют начало, вообще говоря, в других точках. [33]

Радиус-вектор А при вращении проектируется на неподвижную ось ординат Оу. На том же рис. 9 - 10 показана кривая изменения проекции а радиуса-вектора при его вращении. Проследим изменение проекции радиуса-вектора при его полном обороте. Для момента времени / 0 проекции а радиуса-вектора А превращается в точку и, значит, величина этой проекции равна нулю: а - О. [34]

Радиус-вектор направлен от центра поля к рассматриваемой точке. F является силой притяжения. [35]

Радиус-вектор г является диагональю параллелепипеда П с измерениями х, у, г, образованного плоскостями МА МВ, AJC и координатными плоскостями. [36]

Радиус-вектор, соединяющий Солнце с планетой, оме-тает в равные промежутки времени равные площади. [37]

Радиус-вектор от Солнца до планеты заметает равные площади в равные - интервалы времени. [38]

Радиус-вектор г является диагональю параллелепипеда П с измерениями х, у, г, образованного плоскостями MA, MB, MC и координатными плоскостями. [39]

Радиус-вектор каждой точки кривой равен длине отрезка нормали в этой точке. [40]

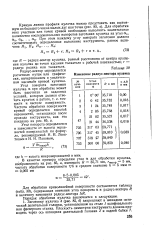Изменение радиус-вектора кулачка. [41]

Радиус-вектор определяется расчетным путем или графически, вычерчиванием в увеличенном масштабе кривой кулачка. [42]

К выводу уравнения движения капли на вращающейся пластине. а-вид на плоскость гх. б - проекция пластины на плоскость ху. в - профиль лопатки. [43]

Радиус-вектор г точки М лежит в плоскости пластины. [44]

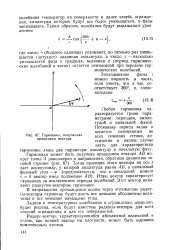Гармоника, получаемая вращением вектора. [45]

Страницы: 1 2 3 4