Радиус-вектор - электрон
Cтраница 1
Радиус-векторы электронов обозначены как г, а заряды их ( отрицательные единичные и одинаковые для всех электронов) для упрощения записи просто не указываются. Радиус-векторы ядер обозначены как 1Ц, а их заряды как Zk Так как при излучении и поглощении электромагнитной энергии сложной молекулы ее центр масс практически не смещается и не появляется момент импульса ( молекула не приходит во вращение как целое), то все относительные движения ядер совершаются лишь в области, близкой к положению минимума соответствующей потенциальной поверхности. [1]
Величина г представляет собой радиус-вектор электрона. [2]
 |
Межмолекулярный потепциал димера ( СН4 а, рассчитанный статистическим методом в работе. [3] |
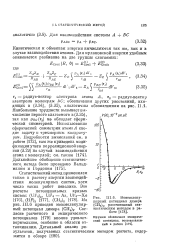
А, г2 - радиус-вектор электрона молекулы ЬС; обозначения других расстояний, входящих в (3.34), (3.35), аналогичны обозначениям на рис. 11.1. Наибольшие трудности вызывает вычисление первого слагаемого в (3.35), так как Рвс ( га) ые обладает сферической симметрией. Использование сферической симметрии атома А сводит задачу к трехмерным квадратурам. [4]
Дипольный момент атома водорода сводится к радиус-вектору электрона: d ег. [5]
Здесь Zi, Z2 - заряды ядер, г - радиус-вектор электронов первого атома, г - радиус-вектор электронов второго атома, причем каждый из них отсчитывается от ядра своего атома. [6]
Здесь Zi, Z2 - заряды ядер, г - радиус-вектор электронов первого атома, г - радиус-вектор электронов второго атома, причем каждый из них отсчитывается от ядра своего атома. [7]
В общем случае а rr ( x Va r yY I г I а поэтому га не является радиус-вектором электрона г в обычном смысле. [8]
Поле будет создавать момент силы, действующий в точках траектории электрона: - е [ х, Щ; здесь через х обозначен радиус-вектор электрона. [9]
Скорость электрона, движущегося по окружности радиуса га, можно представить в виде УСОГОТ, где со - скорость, с которой поворачивается радиус-вектор электрона, т - орт касательной к орбите в той точке, где находится электрон. [10]
Скорость электрона, движущегося по окружности радиуса г0, можно представить в виде v шгот, где ш - скорость, с которой поворачивается радиус-вектор электрона, т - орт касательной к орбите в той точке, где находится электрон. [11]
Поле будет создавать момент силы, действующий в точках траектории электрона: - е [ А:, § ]; здесь через х обозначен радиус-вектор электрона. [12]
Взаимодействие полевых точечных ионов с излучателем в дипольном приближении представимо в терминах электрического ионного микрополя F в предположении, что возмущающие частицы расположены достаточно далеко от излучателя так, что радиус-вектор излучающего электрона много меньше радиусов-векторов возмущающих частиц относительно ядра излучателя. [13]
Так как положение атома ( начало координат) произвольно, мы должны провести усреднение по всем фазам 6; тогда множитель cos26 становится равным Vz - Далее, мы должны усреднить по всем ориентациям атома и, следовательно, заменить хаь 2 У ь на 2Л гв & 2, где г есть радиус-вектор электрона. [14]
Это разложение фактически является рядом Тейлора по степеням малого параметра rt / R, где г4 - радиус-вектор i-то электрона. [15]
Страницы: 1 2