Разбиение - молекула
Cтраница 1
Разбиение молекулы на лоджии представляет собой разбиение трехмерного пространства молекулы на неперекрывающиеся объемы Vi. Определенный вариант заполнения электронами этих объемов ( п электронов в Vi, n2 в V2, n3 в V3) составляет некоторое электронное распределение. Волновая функция позволяет рассчитать вероятность каждого из рассматриваемых распределений. [1]
Разбиение молекулы на фрагменты зависит от физических соображений, которыми руководствуются при выборе этих фрагментов. [2]
 |
Разбиение ВН и ВеН на три лоджии. [3] |
Результаты разбиения молекулы ВН на три наилучшие лоджии обсуждены проф. [4]
В разбиении молекул на отдельные фрагменты существует, однако, элемент произвола, что приводит к весьма большому количеству расчетных схем различной степени обоснованности. Многие из них либо полностью, либо в значительной степени эквивалентны, в связи с чем нет необходимости рассматривать все эти методы. Ниже мы остановимся на некоторых из методов, хотя в наши цели и не входит подробный анализ каждого из них. Для целей данного изложения они играют скорее иллюстративную роль. [5]
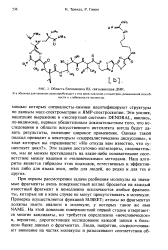 |
Область блеомицина В2, связывающая ДНК. [6] |
При первом рассмотрении задачи разбиения молекулы на значимые фрагменты очень поверхностный взгляд бросается на каждый известный фрагмент и немедленно исключаются любые фрагменты, которые ни в коем случае не могут присутствовать в молекуле. Проверка осуществляется функцией SUBSET; атомы во фрагментах должны иметь аналоги в молекуле, у которых такое же имя NAME. На этой довольно поверхностной первой стадии отвергаются многие кандидаты, но требуется определенно нечеловеческое и, вероятно, дорогостоящее исследование каждой записи в большом банке данных о фрагментах. [7]
Для некоторых из этих систем изучено влияние способа разбиения молекул на группы на точность предсказания фазовых равновесий. [8]
В свою очередь Додель отметил, что одно лишь разбиение молекул на лоджии и описание с помощью только наиболее вероятного распределения не является пределом, и, конечно же, необходимо принимать во внимание сател-литные вероятности, ответственные за корреляцию. Полученное разбиение электронной плотности может быть и не наилучшим в смысле передачи других наблюдаемых величин, поэтому при разработке аддитивных схем необходима большая осторожность. [9]
Проведение плоской разделяющей поверхности через ядро, сопровождающееся лишь незначительным увеличением объема несвязывающей лоджии [ см. несвязывающие заселенности ( Be) - и ( В) - фрагментов в табл. 2 ], определяет лоджии, которые за вычетом основной лоджии будут содержать средние заселенности, равные одному и двум электронам в ВеН и ВН соответственно. Таким образом, интуитивно наиболее вероятное разбиение молекул ВеН и ВН на три лоджии характеризуется радиусом остова г и углом а. Независимое варьирование г и а приводит к минимизации смешанной информационной функции. Тем не менее и в этом случае, сравнивая разбиения на наилучшие лоджии и вириальные фрагменты, мы должны объединить несвязывающую и остовную лоджии, что приведет к ( Be) - фрагменту, и идентифицировать лоджию связи с ( Н) - фрагментом. [10]
Сложная молекула может рассматриваться как ряд известных фрагментов, связанных между собой некоторыми простыми способами. Проблема определения одного из ( вообще говоря, многих) способов разбиения молекулы на фрагменты включает некоторые классические проблемы информатики. Распознавание образов необходимо для того, чтобы удостовериться в том, что фрагмент действительно содержится в молекуле; должна быть разработана оптимальная стратегия поиска, так чтобы выбрать наиболее целесообразное разбиение молекулы на фрагменты среди очень большого числа возможных. Эта проблема известна как задача о ранце, поскольку она сходна с задачей нахождения наилучшего способа упаковки вещей в мешок ограниченных размеров. Мы можем показать, что оптимальное представление фрагментов содержит большие фрагменты, в значительной степени перекрывающиеся. Критерий оптимальности представления выделяет долю всех расстояний в молекуле, имеющихся во фрагментах. Вторичным критерием является то, что в представление включается незначительное число фрагментов. [11]
Как правило, все эти подходы развивались в рамках приближения самосогласованного поля с использованием базисов из достаточно хорошо локализованных атомных орбиталей. Кроме того, коль скоро и атом, и молекула - физические объекты в обычном трехмерном пространстве, то и разбиение молекулы на атомы всегда стремились проводить в том же пространстве, несмотря на то, что при использовании представ-ления волновых функций или их некоторых сверток приходится иметь дело с функциями, заданными в пространстве большего числа измерений: даже матрица плотности первого порядка зависит от шести пространственных переменных. [12]
На рис. 5 сопоставлены линейный и конвергентный ( концептуальный) пути синтеза додекана из пропана. Когда соединяются два фрагмента, наибольшее увеличение сложности наблюдается в результате объединения двух молекул одинаковой сложности. В терминологии ретросинтеза наибольшее упрощение возникает при разбиении молекулы искомого продукта на две половины равной сложности. [13]
Сложная молекула может рассматриваться как ряд известных фрагментов, связанных между собой некоторыми простыми способами. Проблема определения одного из ( вообще говоря, многих) способов разбиения молекулы на фрагменты включает некоторые классические проблемы информатики. Распознавание образов необходимо для того, чтобы удостовериться в том, что фрагмент действительно содержится в молекуле; должна быть разработана оптимальная стратегия поиска, так чтобы выбрать наиболее целесообразное разбиение молекулы на фрагменты среди очень большого числа возможных. Эта проблема известна как задача о ранце, поскольку она сходна с задачей нахождения наилучшего способа упаковки вещей в мешок ограниченных размеров. Мы можем показать, что оптимальное представление фрагментов содержит большие фрагменты, в значительной степени перекрывающиеся. Критерий оптимальности представления выделяет долю всех расстояний в молекуле, имеющихся во фрагментах. Вторичным критерием является то, что в представление включается незначительное число фрагментов. [14]
Другие приложения понятия бинарного отношения 9J в теоретической химии связаны с различными способами интерпретации элементов множества 2ft, па котором определяется это отношение. При формальном описании химических реакций ( например, внутримолекулярных перегруппировок, последовательных замещений, процессов деструкции п др.) элементами множества 2ft являются продукты реакции. Разбиение молекул на пары, соответствующие выбору множества ЭЙ, может проводится с учетом имеющихся представлений об элементарном акте реакции, характерном для исследуемой задачи. [15]
Страницы: 1 2