Разбиение - фазовая плоскость
Cтраница 1
Разбиение фазовой плоскости на листы для рассматриваемого примера показано на рис. 6.3, а. В кружках показаны соответствующие каждому листу значения jift. Такая интерпретация многолистной фазовой плоскости иногда оказывается весьма полезной. [1]
Соответствующие этим типам особых элементов структуры разбиения фазовой плоскости на траектории показаны на рис. 3.2 - 3.5. На рис. 3.2 изображены три последовательные фазы изменения поведения фазовых траекторий в окрестности двух простых особых точек: узла 01 н седла О. [2]
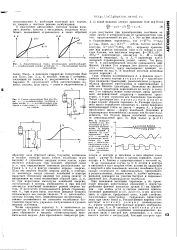 |
Схемы генераторов Ван дер Поля. а - с колебательным контуром в цепи анода. б - с колебательным контуром в цепи сетки. в - характеристика лампы. [3] |
При изменении величины параметра i не происходит никаких качественных изменений в структуре разбиения фазовой плоскости ур-ния ( 1) на траектории - при любом и0 в системе имеются единств, состояние равновесия ( ж0, dx / dt - Q), к-рое неустойчиво, и единств, предельный цикл, к-рый устойчив. Качественные перестройки - бифуркации происходят лишь при смено знака и. Рассмотренная картина соответствует мягкому режиму возникновения А. В системах сжестким режимом возбуждения колебания самопроизвольно нарастают лишь с нек-рой нач. [4]
При этом оказалось, что если ограничиться так называемыми грубыми системами, то качественная картина разбиения фазовой плоскости на траектории полностью определяется конечным числом ее особых траекторий: состояний равновесия, предельных циклов и сепаратрис седловых состояний равновесия. [5]
Ламерея, построенная на этих кривых, может содержать самое большее две ступеньки. Соответствующее разбиение фазовой плоскости ху на траектории для рассматриваемого случая 0 с Р 1 показано на рис. 4.38. Рассмотрение случая р 0 проводится аналогично. Функция последования по-прежнему определяется соотношениями (4.51), а диаграмма Ламерея имеет вид, показанный на рис. 4.39. Таким образом, в случае Р О точечное отображение (4.51) имеет единственную неподвижную точку, которая является устойчивой. [6]
В этом случае топологическая структура разбиения фазовой плоскости не отличается от только что рассмотренной, но устойчивый предельный цикл увеличивается, а неустойчивый - уменьшается. [7]
В простейшем случае фазовая поверхность представляет собою обычную плоскость с декартовыми координатами х, у, а функции Р ( х, у) и Q ( х, у) являются аналитическими на всей плоскости. Основная задача исследования динамической системы состоит в том, чтобы выяснить качественную картину разбиения фазовой плоскости па траектории или, другими словами, установить топологическую структуру этого разбиения. [8]
Отсекая особые случаи, приходим к двум существенно разным локальным картинкам, представленным на рис. 7.2, на которых изображены окрестности простых устойчивого и неустойчивого периодических движений После этого удается склеить все локальные картинки вместе и прийти к полной ясности в отношении вида общего разбиения фазовой плоскости на траектории. Некоторые из них изображены на рис. 7.3 Это означает полное исследование вопроса о структуре разбиения фазовой плоскости на фазовые траектории. [9]
На рис. 7.102 и 7.100 изображены поведения последовательных преобразований точек плоскости в плоскость при обычном и стохастическом синхронизмах. Эти картинки похожи на изображение разбиения фазовой плоскости на траектории. Однако на них кривые изображают не траектории движения фазовых точек. Траекторией движения точки для точечного отображения плоскости в плоскость является последовательность точек, в которой каждая следующая точка получается преобразованием предыдущей. Поэтому, если на такой кривой лежит какая-нибудь точка последовательности, то на ней лежат и все ее точки, причем они расположены на ней с сохранением порядка. Порядок следования точек последовательности определяет некоторое направление на инвариантной кривой, которое на рис. 7.102 и 7.100 отмечено стрелками. [10]
Отсекая особые случаи, приходим к двум существенно разным локальным картинкам, представленным на рис. 7.2, на которых изображены окрестности простых устойчивого и неустойчивого периодических движений. После этого удается склеить все локальные картинки вместе и прийти к полной ясности в отношении вида общего разбиения фазовой плоскости на траектории. Некоторые из них изображены на рис. 7.3. Это означает полное исследование вопроса о структуре разбиения фазовой плоскости на фазовые траектории. [11]
Из физических соображений очевидно, что в дифференциальных уравнениях (3.1), описывающих движение реальной физической системы, ни один из учитываемых нами факторов не может оставаться абсолютно неизменным во времени. Следовательно, правые части уравнений (3.1), вообще говоря, изменяются вместе с входяищми в них физическими параметрами. Однако если эти изменения достаточно малы, то, как показывает практика, физическая система как бы не замечает этих изменений, качественные черты ее поведения сохраняются. Поэтому, если мы хотим, чтобы уравнения (3.1) отобразили эту особенность, нужно придать им свойство грубости, а именно: при малых изменениях параметров должна оставаться неизменной качественная структура разбиения фазовой плоскости на траектории. [12]
Из физических соображений очевидно, что в дифференциальных уравнениях (3.1), описывающих движение реальной физической системы, ни один из учитываемых нами факторов не может оставаться абсолютно неизменным во времени. Следовательно, правые части уравнений (3.1), вообще говоря, изменяются вместе с входящими в них физическими параметрами. Однако если эти изменения достаточно малы, то, как показывает практика, физическая система как бы не замечает этих изменений, качественные черты ее поведения сохраняются. Поэтому, если мы хотим, чтобы уравнения (3.1) отобразили эту особенность, нужно придать им свойство грубости, а именно: при малых изменениях параметров должна оставаться неизменной качественная структура разбиения фазовой плоскости на траектории. [13]
Страницы: 1