Разбиение - вектор
Cтраница 1
Разбиение вектора у ( х) на два вектора ух ( х) и у2 ( х) может быть выполнено произвольно. [1]
Разбиение вектора у ( х) на два вектора ух ( я) и у2 ( х) может быть выполнено произвольно. [2]
Однако разбиение вектора т на два слагаемых, которое нами сделано, не является единственным. [3]
Ги 0, и соответствующие ему разбиения вектора X и системы 7г ( t, х, X) 0, на подвекторы ( Х, Х2) и подсистемы fr ( f, х, X) О, г 2 (, х, X) 0, где Гп д7Г / ЗХГ. [4]
Проведем посекторное ( по предприятиям) разбиение векторов лимитов общих ресурсов. [5]
Способ перехода к цели первого типа путем разбиения векторов Wj) на удовлетворительные и неудовлетворительные. [6]
Такую запись можно считать недостаточно четкой в том смысле, что по форме она связана с разбиением вектора смещений на две составляющие. [7]
В случае линейной возмущенной системы [4] приведение к регулярной форме относительно внешних возмущений заключалось в перестановке строк и разбиением вектора yl на подвекторы, из которых последовательно получают, как линейную комбинацию, зависящую от матриц с постоянными коэффициентами, новые компоненты вектора состояния с нужными свойствами. Для приведения нелинейных уравнений ( 3) к регулярной форме относительно возмущений потребуется выполнить интегральное преобразование, поскольку матрицы перед возмущениями нелинейные. В этом состоит отличие решения задачи для нелинейной системы по сравнению с линейной системой. [8]
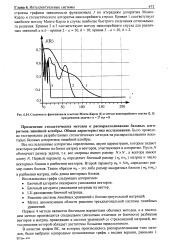 |
Сходимость функционала в методе Монте-Карло ( 1 и методе наискорейшего спуска ( 2 3. [9] |
Первые 4 метода являются блочными вариантами обычных методов, а в последнем методе производится специальное ( несколько отличное от блочного) разбиение векторов и матриц, приводящее к системе уравнений со стреловидной матрицей, метод решения которой обладает достаточно большим параллелизмом. [10]
VI была получена разностная схема, которой соответствует система линейных алгебраических уравнений с пятпднагоиалыюй матрицей порядка N ( ЛГ1 - 1) ( Ла - 1), где / i - J, Л з - 1 - число внутренних узлов по каждому направлению. При разбиении вектора неизвестных на блоки, содержащие по Nt - J элементов, мы получим запись системы с блочшьтрех-дпагопальной матрицей, число блоков которой равно Л а-I. [11]
 |
Дерево бинарных классификаторов образов. [12] |
Бинарные классификаторы образов были расположены по ветвящейся схеме. Каждый бинарный классификатор обучали разбиению векторов образов на две категории по схеме, изображенной на рис. 4.4. При построении шести классификаторов были использованы только те спектры, которые относились к соответствующей точке ветвления. Прогнозирующую способность каждого весового вектора определяли аналогично на контрольной выборке из 172 векторов. Результаты такого обучения и данные о прогнозирующей способности приведены в табл. 4.17. Затем обученные весовые векторы были использованы для классификации по главной программе ветвящейся классификации. [13]
Все исследованные алгоритмы определялись двумя параметрами, которые задают некоторое разбиение на блоки матриц и векторов, участвующих в алгоритме. Пусть N обозначает размер задачи, т.е. все матрицы имеют размер NxN, а вектора имеют длину N. Первый параметр пь определяет блочный размер ( nbxnb) матриц и число векторных блоков в разбиении векторов. Второй параметр mb N / nb определяет размер самих блоков. [14]
Все исследованные алгоритмы определялись двумя параметрами, которые задают некоторое разбиение на блоки матриц и векторов, участвующих в алгоритме. Пусть jV обозначает размер задачи, т.е. все матрицы имеют размер NxN, а вектора имеют длину N. Первый параметр п /, определяет блочный размер ( пь х пь) матриц и число векторных блоков в разбиении векторов. Второй параметр ть N / nb определяет размер самих блоков. [15]
Страницы: 1 2