Величина - отношение - толщина
Cтраница 2
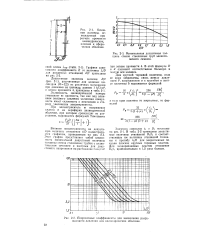 |
Минимальная допустимая толщина стенок стеклянных труб эллиптического сечения.| Поправочные коэффициенты для вычисления разрушающего давления для цилиндрических оболочек. [16] |
В табл. 2 - 2 приведены допустимые величины отношений Dt / ti и соответствующие им величины отношений толщины к прогибу ti / d для закрепленных по краям плоских круглых торцевых пластин. Для незакрепленных пластин отношение Di / ti приблизительно в 1 2 раза больше. [17]
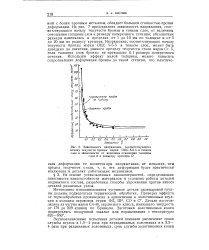 |
Зависимость напряжения, соответствующего. [18] |
На рис. 7 представлена зависимость напряжения, соответствующего началу текучести бронзы в тонком слое, от величины отношения толщины слоя к размеру поперечного сечения; абсолютные размеры изменялись в пределах от 1 до 10 мм по толщине и от 5 до 20 мм по радиусу крешера. Напряжение, соответствующее началу текучести бронзы марки ОЦС 5 - 5 - 5 в тонком слое, может быть доведено до значения, равного пределу текучести стали марки Ст. [19]
Единственным, что действительно известно, является-то, что для тонких оболочек напряжения oz будут малы по сравнению с напряжениями оа и о. Рассмотрим, например, влияние величины отношения толщины к радиусу оболочки на связь между этими напряжениями. R, нагруженного равномерно распределенным внутренним давлением р; в этом случае среднее окружное напряжение равно. [20]
Теперь рассмотрим способ гнутья с односторонним стеснением в гибе. По мере увеличения диаметра и уменьшения величины отношения толщины стенки трубы к диаметру процесс гнутья усложняется. Овализация трубы в гибе увеличивается и происходит потеря устойчивости стенок. [21]
Указанное геометрическое рассмотрение показывает, что поглощение фаз регулируется толщиной и объемными отношениями гидрофильной и липофильной частей молекул ПАВ. Экспериментальные данные ( рис. 23.12) показывают, что эти параметры являются независимыми в насыщенных мицелпярных системах. Геометрическая модель показывает также, что относительные величины толщины и объемных отношений определяют радиус капли и, следовательно, кривизну поверхности раздела. В предположении существования двойного слоя вокруг капли заключено утверждение, что кривизна поверхности раздела является результатом различий в давлении по разные стороны от двойного слоя. На рис. 23.14 представлены результаты такого анализа насыщенных мицелпярных систем. Верхние уравнения описывают связь между поверхностным натяжением и давлением на поверхность раздела в насыщенных микроэмульсиях. Давления на поверхность раздела определяются через величины относительной сжимаемости головок и хвостов молекул ПАВ. Из этих уравнений видно, что величина отношения толщин головки к хвосту молекул ПАВ в насыщенных микроэмупьсиях зависит от межфазного натяжения и сжима - емостей головок и хвостов молекул ПАВ. [22]
Страницы: 1 2