Величина - средняя квадратическая ошибка
Cтраница 1
Величины средних квадратических ошибок во всех случаях допустимо малы, так что линия регрессии достаточно точно воспроизводит наблюдаемые значения условной средней Yx. Исследования показали, что при изменении абсолютной величины тв.п. m начиная с 30 сек и дальше в сторону увеличения, происходит рост среднего размера, подчиняющийся определенной прямо пропорциональной закономерности, тогда как при непродолжительном предварительном подогреве ( 30 сек) изменения размеров происходят скачкообразно. [1]
Рассчитаем величину средней квадратической ошибки, которую можно допустить в положении рабочей оси в плоскости сбойки, если для тоннеля с тюбинговой обделкой величина А, заданная проектом, равна 100 мм. [2]
На величину средней квадратической ошибки в большей степени оказывают влияние крупные по абсолютным значениям ошибки. [3]
Из фурмулы ( 6) видно, что величина средней квадратической ошибки выборочной средней зависит от величины OQ - среднего квадратического отклонения СВ от генеральной средней распределения. Однако на практике значение а0 нам неизвестно. [4]
При расчетах допусков влияния отдельных источников ошибок будем исходить из величины средних квадратических ошибок углов, установленных для соответствующих разрядов полигонометрии. [5]
При селекции из ряда в ряд пропускается только некоторое число самых регулярных переменных, степень регулярности которых оценивается по величине средней квадратической ошибки ( средней для всех выбираемых в каждом поколении переменных или для одной самой точной переменной) на отдельной проверочной последовательности данных. Иногда в качестве показателя регулярности используется коэффициент корреляции. Ряды селекции наращиваются до тех пор, пока регулярность повышается. Рекомендуется остановить селекцию несколько раньше достижения полного минимума, что дает более простые и достоверные уравнения. [6]
Изучение характера воздействия на автоматическую систему станок-инструмент-деталь-измерительный прибор является важнейшей задачей при решении проблемы обеспечения заданной динамической точности обработки деталей машин и создания надежно работающих станков, которые должны автоматически и непрерывно рассчитывать величину средней квадратической ошибки обработки, устанавливать условия ее минимума и обеспечивать поддержание этого минимума длительное время. [7]
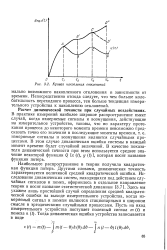 |
Кривая накопления отклонений. [8] |
Другими словами, динамическая точность характеризуется величиной средней квадратической ошибки. Здесь мы укажем лишь простейший случай определения средней квадратической ошибки на выходе измерительного устройства, когда измеряемый сигнал и помехи являются стационарными в широком смысле и эргодическими случайными процессами. [9]
Предположим теперь, что эти процессы нормальные. Тогда нетрудно убедиться, что добавление нелинейных элементов к оптимальному линейному фильтру не может уменьшить величины средней квадратической ошибки. [10]
 |
Частотные ха-рактеристики и спектральные плотности сигналов. [11] |
Подынтегральные выражения представляют собой квадрат модуля дробно-рациональной функции. Каждый из интегралов можно вычислить, например, определив корни знаменателя и разложив подынтегральное выражение на простейшие дроби. Имеются и другие способы вычисления М е2, которые не требуют определения корней и позволяют получить в явном виде связь между параметрами, входящими в выражение для Sg ( ш), и величиной средней квадратической ошибки. [12]
В ряде случаев чувствительный элемент прибора автоматического контроля, управления или регулирования размеров в машиностроении испытывает непрерывно изменяющиеся воздействия. При этом оказывается невозможным выбрать наиболее типичное или наиболее вредное воздействие и построить по нему график переходного процесса. Сохраняет значение только максимальное отклонение, однако величина и знак его могут быть неизвестными. В таких случаях приходится оценивать средние значения максимального отклонения изучаемой величины. Это отклонение должно вписываться в поле допуска на изучаемую величину. Если среднее значение отклонения будет выходить из поля допуска, то в системе появится средняя ошибка, которую обычно оценивают величиной средней квадратической ошибки. [13]
Страницы: 1