Величина - управляющий параметр
Cтраница 1
Величины управляющих параметров, при которых изменяется природа нелинейной динамической системы. Такая система может бифурцировать или совершить переход от устойчивого состояния к турбулентности. Примером может служить соломинка, переломившая верблюжью спину. [1]
Во время проведения технологического процесса величина управляющего параметра изменяется. Это изменение носит немонотонный характер и в ряде случаев имеет один или несколько экстремумов. Экстремальное изменение управляющего параметра указывает на наличие критических точек в нефтяной системе. В критических точках может осуществляться либо структурный фазовый переход, либо резкое изменение состава нефтепродукта, либо иные следствия. В любом случае такие критические точки являются наиболее удобными местами, в которых возможно осуществлять точечную регулировку параметров технологического процесса в целом. Суть этой регулировки заключается в том, что в точках экстремального изменения управляющего параметра нефтяная система становится аномально чувствительной к внешним воздействиям. [2]
В случае системы автоматической, стабилизации величина управляющего параметра неизменна. [3]
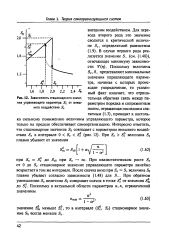 |
Зависимость стационарного значения управляющего параметра 50 от внешнего воздействия Зе. [4] |
Поскольку величины Se, S - представляют минимальные значения управляющего параметра, начиная с которых происходит упорядочение, то указанный факт означает, что отрицательную обратная связь между параметром порядка и сопряженным полем, отражаемая последним слагаемым (1.3), приводит к настолько сильному понижению величины управляющего параметра, которое только на пределе обеспечивает самоорганизацию. Интересно отметить, что стационарное значение So совпадает с параметром внешнего воздействия Se в интервале 0 Se S. [5]
Принцип золотой пропорции является цементирующим принципом, который устанавливает гармоничные соотношения между действием приведенных выше принципов. В результате изменения величины управляющих параметров до критических значений происходит смена доминирующего положения одного из принципов. Например, достижение критического состояния может означать, что приоритет воздействия на нефтяную систему переходит от принципа фрактальности к принципу ограничения. [6]
Для случаев - и Ч и получены аналитические выражения, определяющие количественную связь г зжду входными параметрами электролиза и качеством образующейся электрощелочи при статическом и динамическом режимах электролиза. Аналитически показана зависимость коэффициентов модели от величины управляющего параметра ( расхода рассола) и от времени работы электролизера, т.е. подтверждены нелинейность и нестационарность процесса. Полностью модель диафрагменного электролиза, включающая уравнения для расчета некоторых физико-химических характеристик состава электролита, состоит из 49 алгебраических и дифференциальных уравнений. [7]
В теоретическом отношении этот метод наиболее исследован, ему посвящено множество публикаций и монографий. В этих работах предпринята попытка прогнозировать как величины оптимальных управляющих параметров, так и значения технико-экономических показателей будущего рейса. Этот метод основан на аналитическом исследовании основных закономерностей процесса бурения или его математических моделей и прогнозировании на этой основе всех результатов взаимодействия долота с породой, включая и время пребывания долота на забое. [8]
При прочих равных условиях ( при одном и том же уровне напряжения ( а0)) два многопараметрических цикла нагружения будут отличаться между собой величиной управляющего параметра а, который пропорционален плотности энергии разрушения. Напротив, различие в кинетике усталостных трещин для одного и того же материала при двух разных уровнях одноосного напряжения пульсирующего цикла может быть устранено за счет изменения других параметров цикла нагружения. [9]
Первым и важнейшим этапом математического моделирования, определяющим успех всей последующей работы, является расчленение исследуемого процесса на его составные уровни, установление их взаимосвязи. Это позволяет построить структурную схему процесса, которая оказывается иерархической, поскольку законоыер - ности протекания элементарных актов и явлений на более высоким уровне могут быть поняты и объяснены на основе знания закономерностей нижних уровней. При экспериментальном исследовании этого уровня обычно лишь констатируется связь между величинами управляющих параметров и результатом их воздействия без объяснения причин наблюдаемых закономерностей. [10]
Их физическая сущность сводится к тому, что через них можно полностью описать поведение системы при любом многопараметрическом внешнем воздействии. Они остаются неизменными во времени, если неизменными во времени остаются внешние условия воздействия на систему. Из этого следует, что управлять поведением открытой системы во времени через управляющие параметры можно только в том случае, если установлена однозначная связь между законом изменения этих параметров во времени и законом изменения внешних условий воздействия на систему. При этом чрезвычайно важно, что одна и та же величина управляющего параметра достигается при различной комбинации условий внешнего воздействия на открытую систему. [11]
Эксплуатационное воздействие на элемент конструкции реализуется при переменных параметрах цикла нагружения во времени. Порождаемый при таком нагружении поток энергии является нестационарным. Такой вид нагружения, согласно принципам синергетики об упорядоченности ступеней самоорганизации, позволяет осуществлять многократное повторение тех или иных механизмов эволюции, присущих данной системе. Применительно к распространению усталостных трещин это означает, что причины переходов от одних механизмов разрушения к другим могут быть следствием изменения величины управляющего параметра, однако в направлении роста трещины можно реализовать только те механизмы, которые характеризовали рост трещины при стационарном режиме нагружения. [12]
Система обладает определенной инерцией и при достаточно высоком уровне энергетического воздействия приспосабливается к новой ситуации в течение некоторого времени. Классическим примером служат релаксационные явления. Если время приспособления системы к новой ситуации меньше, чем время, когда реализуется новое воздействие, то в каждом случае можно использовать одни и те же эволюционные уравнения для описания поведения системы после каждого воздействия с введением некоторой константы, учитывающей новое состояние системы. Однако в реальной ситуации нагружение элемента конструкции реализуется таким образом, что при переходе с одного уровня нагружения на другой имеет место развитие нелинейных процессов взаимодействия нагрузок, протекающих последовательно в результате каждого изменения режима. Поэтому уравнение (2.40) следует рассматривать в общем виде с добавками на нелинейность, характеризующими дополнительное изменение величины управляющего параметра при переходе от одного уровня или величины воздействия на другой. [13]
В типичном случае осциллятора с одной степенью свободы, при приближении управляющего параметра к значению, критическому для хаотического движения, возникают субгармонические колебания. Явление внезапной перестройки движения при изменении параметра называется бифуркацией. На рис. 4.5 приведен пример экспериментальной бифуркационной диаграммы. Такие диаграммы получаются в эксперименте с помощью временной выборки измерений движения, как при построении отображения Пуанкаре, и отображения этой выборки на осциллографе, как показано на рис. 4.5. Здесь по горизонтальной оси откладывается величина управляющего параметра, например амплитуда или частота возбуждения, а по вертикальной - значения координаты из временной выборки. По сути дела эта диаграмма описывает целую серию экспериментов, каждый из которых проводится при определенном значении управляющего параметра. Такую диаграмму можно получить довольно быстро, если есть возможность автоматического изменения управляющего параметра, например с помощью компьютера и преобразователя цифрового сигнала в аналоговый. [14]
Страницы: 1