Случайный разброс - параметр
Cтраница 1
Случайные разбросы параметров оказывают существенное влияние на точность ее работы. Поэтому при анализе ДСАУ необходимо учитывать указанные выше косвенные возмущения. [1]
Случайный разброс параметров объекта обусловлен большим количеством факторов технологического и эксплуатационного характера. Среди этих факторов обычно трудно выделить преобладающий. В такой ситуации, согласно центральной предельной теореме Ляпунова, закон распределения параметров очень близок к нормальному. [2]
Случайный разброс параметров объекта обусловлен большим количеством факторов технологического и эксплуатационного характера. [3]
Требуется определить влияние случайного разброса параметров 11, 12, is, 21, 22, 32, 35, вызванного погрешностями изготовления и настройки отдельных элементов системы автоматического управления, на статистику разброса динамических характеристик всей системы по каналу возмущения в переходном режиме. Это необходимо для правильного выбора полей допусков настроек элементов системы управления в условиях серийного производства. Таким образом, требуется найти математическое ожидание mv ( t) и дисперсию Dp ( t) для выходного сигнала ( p ( t) на интервале времени t 0 20 с, немного превышающем время переходного процесса. [4]
При проектировании также учитывается случайный разброс параметров элементов объекта, обусловленный технологическим процессом изготовления. Все процессы, происходящие в объекте, также случайны и могут быть оценены вероятностными и статистическими характеристиками: вероятностью выполнения тех или иных требований, корреляционной функцией, спектральной плотностью, математическим ожиданием, дисперсией и др. Анализ функционирования объекта в этом случае требует построения вероятностной математической модели. Однако такая модель весьма сложная и ее использование при проектировании требует больших затрат машинного времени. Поэтому ее применяют чаще на заключительном этапе проектирования. [5]
Второе слагаемое отражает влияние случайного разброса параметра. Следует отметить, что и в первом слагаемом случайный разброс деформирует спектр и уровень спектральной плотности. [6]
Однако в современных сложных системах управления случайный разброс параметров, вызванный как условиями изготовления элементов ( разброс допусков), так и условиями эксплуатации ( климатические и механические воздействия), часто приводит не только к значительным ошибкам, но в ряде случаев к потере устойчивости и нарушению качества переходных процессов в системе. [7]
 |
Разомкнутая схема управления. [8] |
В принципе, в таких моделях возможно учитывать и случайный разброс параметров передаточной функции человека, обусловленный тем, что система строится не под одного оператора, а под совокупность операторов, имеющих индивидуальные особенности. [9]
Таким образом, разработка метода анализа динамической точности при случайном разбросе параметров диктуется как необходимостью общего анализа точности, так и надежности системы. Здесь имеет место пересечение этих двух направлений анализа динамических систем. [10]
Рассмотрим пример синтеза корректирующего устройства электрогидравлического усилителя типа УЭГ-С с учетом возможного случайного разброса параметров синтезируемого корректирующего устройства. [11]
В (2.222) - (2.224) буквами а, 6, fc0c с соответствующими индексами обозначены детерминированные составляющие коэффициентов, а буквами а, 6, koc - их некоррелированные случайные составляющие с нулевыми средними значениями, учитывающие случайный разброс параметров объекта, корректирующего устройства и цепи обратной связи. [12]
Таким образом, формулы ( 72), ( 78), ( 79), ( 83), ( 91) и ( 92) позволяют производить расчет динамической точности при наличии параметрического возмущения в виде случайного разброса параметров системы управления. [13]
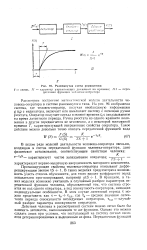
Интервал наблюдения над этой системой должен быть значительно длиннее интервала корреляции процесса, характеризующего параметрическое возмущение. Определим влияние случайного разброса параметра, находящегося в прямой цепи замкнутой динамической системы. В данном случае изменение параметра обусловлено факторами, не зависящими от управляющего внешнего воздействия, поэтому взаимная корреляция между процессами v ( t) и g ( t) отсутствует. [14]
 |
Структурная схема модели СЧМ со случайными параметрами. [15] |
Страницы: 1 2