Развертка - переход
Cтраница 4
 |
Развертка усеченного конуса. [46] |
Продолжая стороны а-б и в-г до пересечения, находят точку О, из которой радиусами Оа и Об проводят концентрические дуги; откладывая от точки а на дуге радиуса Оа величину кО, а на дуге радиуса Об от точки б величину, равную периметру квадрата, получают соответственно точки д и е, которые соединяют прямой, в результате чего получают искомую развертку перехода а, б, г, е, д, в. К полученному контуру добавляют припуски на фальцы и на отбортовку на фланцы. [47]
 |
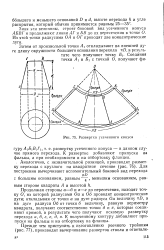
Построение развертки перехода с круглого сечения на овальное с прямой вставкой. [48] |
Переход с круглого сечения на овальное. Развертка перехода выполнена способом триангуляции. По натуральным величинам образующих ( ребер), диагоналей и хорд оснований строят развертку поверхности. На рис. 41, в представлена 1 / 4 часть этой поверхности. [49]
Для построения развертки перехода должны быть заданы размеры оснований ( стороны прямоугольника и диаметр верхнего основания), высота перехода и величина смещения оснований относительно друг друга. Построение развертки данного перехода делается аналогично ранее рассмотренным случаям развертки переходов без смещения оснований. [50]
Ниже приводится метод построения разверток переходов с помощью составленных нами таблиц, значительно ускоряющих и упрощающих процесс разметки. В главе II приведены примеры 18 - 21 построения разверток переходов ( стр. [51]
Существует ошибочное представление, что заданная поверхность перехода с основаниями круглого сечения, не параллельными друг другу, есть коническая поверхность, при которой все образующие этой поверхности при своем продолжении пересекутся в одной точке. Это, как видно, приводит к неправильному способу развертки заданного перехода к усеченному круговому конусу. [52]
По этому методу окружности обоих оснований переходов делятся на равные части. Точки деления соединяются попарно и наискось друг с другом, разбивая таким образом всю поверхность перехода на треугольники. В дальнейшем построение развертки перехода будет сведено к построению истинной величины ряда треугольников, образующих поверхность перехода по трем сторонам. [53]
Чтобы максимально упростить труд разметчика, мы составили табл. 11 - 14, по которым определяются все размеры, необходимые для построения развертки переходов. Основанием для составления таблиц послужили выведенные нами формулы. На рис. 33 - 36 указаны виды разверток переходов, как прямых, так и косых, а в гл. [54]
Для построения развертки перехода должны быть заданы размеры оснований ( стороны прямоугольника и диаметр верхнего основания), высота перехода и величина смещения оснований относительно друг друга. Построение развертки данного перехода делается аналогично ранее рассмотренным случаям развертки переходов без смещения оснований. [55]
Для этого на проволоке ( или шнуре) отмеряют длину L, а затем, изогнув проволоку, прикладывают ее к дуге от точки А. Соединяя точки А1 и Б1 с вершиной О, пересекаем малую дугу в точках / и Bv Полученная фигура А, Б1, Blt Г, является разверткой перехода. [56]
Большую группу составляют переходы с комбинированной поверхностью, состоящей из сочетания плоских и кривых поверхностей. К ним относятся переходы с прямоугольного или квадратного сечения на круглое или наоборот. Переходы этого вида могут быть симметричными и несимметричными. Так как развертка переходов с комбинированной поверхностью строится приведенным выше методом треугольника, то в дальнейшем нет смысла подробно останавливаться на повторении отдельных приемов этого метода. На рисунках дано последовательное вычерчивание развертки путем построения треугольников в истинную величину по трем сторонам. [57]
Для получения линий пересечения достаточно отложить по образующим действительные величины прямых и по полученным точкам определить развертку линии пересечения. Пользуясь этим общим методом, можем легко получить развертку любой сложности фигуры. Для нашего случая сделано построение ответвления тройника. Особенно часто приходится прибегать при развертках всевозможных переходов. Точность раскроя зависит от тщательности разбивки фигуры на отдельные треугольники. В дальнейшем все сложные случаи разверток выполнены приведенным выше методом, но пояснение дано в пооперационной последовательности - способом, наиболее доходчивым к пониманию процесса построения развертки. [58]
В действительности переход представляет случайную поверхность, и развертка такой поверхности должна строиться для таких фасонных частей общим методом замены кривой поверхности многогранником. Для этого каждую из окружностей основания делим на равное число частей, точки деления которых соответственно соединяем прямыми линиями - образующими этой поверхности. Полученные четырехугольники не являются плоскими, так как хорды, стягивающие дуги окружностей, не лежат в одной плоскости. Проведя диагонали на этих участках кривой поверхности, расчленяем ее на составляющие треугольники, построение которых по трем сторонам истинной длины позволит произвести развертку перехода. [59]
Из середины отрезка аб восстанавливают перпендикуляр, на котором откладывают высоту перехода h и через ее конец проводят горизонтальную прямую. На этой прямой откладывают отрезок вг, равный диаметру верхнего основания конуса. Затем радиусом Оа проводят дугу, на которой от произвольной точки А откладывают вначале половину ширины большей стороны нижнего основания перехода, затем ширину меньшей стороны, потом большей и еще раз меньшей стороны основания и половину большей стороны осмеивания. После этого радиусом Об очерчивают дугу. О, получают развертку АСДБ перехода. [60]
Страницы: 1 2 3 4 5