Средняя логарифмическая разность - температура
Cтраница 3
При определении времени нагрева величину потерь в окружающую среду находят, пользуясь средней логарифмической разностью температур в начале и конце процесса. [31]
 |
Изменение температур теплоносителей. а - при прямом токе. б - при противотоке. в - при изме. [32] |
Если начальные и конечные температуры обоих теплоносителей одинаковы, то в случае противотока средняя логарифмическая разность температур будет больше, чем при прямотоке. [33]
Величина температурного напора, усредненная по поверхности, или, как часто называют, средняя логарифмическая разность температур для различных относительно друг друга движений теплоносителей, разделенных между собой стенкой, определяется по известным формулам. [34]
Решение: По условию задачи коэффициент теплопередачи сильно меняется вдоль поверхности теплообмена, поэтому среднюю логарифмическую разность температур применить нельзя. [35]
К - коэффициент теплопередачи, Вт / ( м2 - К); тСр - средняя логарифмическая разность температур. [36]
К - коэффициент теплопередачи, ккал / ( м - ч-град); ср - средняя логарифмическая разность температур, С. [37]
При постоянных с0, св и k приведенное уравнение легко интегрируется, давая выражение для средней логарифмической разности температур. Интегрирование уравнения ( 2 - 1) в общем случае затруднительно, так как входящие в него теплоемкости обоих потоков с0 и св, а также коэффициент теплопередачи k являются сложными функциями температур обоих потоков. [38]
Такой результат объясняется тем, что в сушилках рассматриваемого типа движущей силой переноса тепла является не средняя логарифмическая разность температур, а некоторая другая величина, не зависящая от начальной температуры теплоносителя. [39]
Решение рассмотренной задачи осуществляется значительно проще при использо: вании соотношения между е и jV, чем на основании средней логарифмической разности температур: в первом случае возможно прямое решение, а во втором случае необходим ряд последовательных приближений, что усложняет решение и делает его трудоемким. [40]
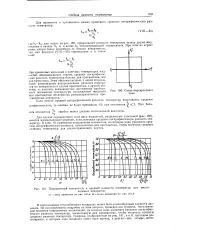 |
Схема перекрестного тока.| Поправочный множитель к средней разности температур для многоходовых аппаратов. а - схема движения по 162 а. б - схема движения по 162 6. [41] |
Для случая перекрестного тока двух жидкостей, разделенных пластиной ( рис. 160), имеется математическое решение, использующее среднюю логарифмическую разность температур. В табл. 61 приведены поправочные множители, на которые надо умножить среднюю логарифмическую разность, вычисленную для противотока, чтобы получить среднюю разность температур для рассматриваемого случая. [42]
Умножением величины средней разности температур, полученной по уравнению ( 42), на поправочный коэффициент ед получаем значение расчетной величины средней логарифмической разности температур А ср. [43]
Здесь через Ал обозначена суммарная наружная поверхность внутренней трубки, а величина ( Т /, - Тс) п представляет собой среднюю логарифмическую разность температур между двумя потоками. Формулы (14.28) и (14.29), описывающие скорость передачи тепла от горячего потока к холодному через стенку теплообменника, находят широкое применение в инженерной практике. Следует отметить, что указанные соотношения не содержат в явном виде объемных скоростей потоков и могут быть использованы для описания как прямоточных, так и противоточных систем. [44]
Вследствие небольшой разности температур масла на входе и выходе из маслоохладителя ( обычно 4 - 5) нет никакого смысла пользоваться средней логарифмической разностью температур при определении общего коэфициента теплопередачи. [45]
Страницы: 1 2 3 4 5