Абсолютная величина - отношение
Cтраница 1
Абсолютная величина отношения М / М0 отражает симметрию условий текучести. [1]
Здесь абсолютная величина отношения взята для того, чтобы не возникала путаница из-за правила знаков для напряжения, а также из-за того, что инжектированный заряд может быть как положительным, так и отрицательным. Эффективное значение инжектированного заряда следует брать потому, что из-за распределенного характера этого заряда он не весь одинаково участвует в образовании емкости. Поэтому приходится проводить какое-то усреднение. [2]
Абсолютная величина отношения абсолютной погрешности измеряемой величины к ее приближенному значению называется относительной погрешностью. [3]
Рассогласование хода - абсолютная величина отношения разности действительного и приведенного ходов к величине условного хода в рабочих условиях, выраженная а процентах. [4]
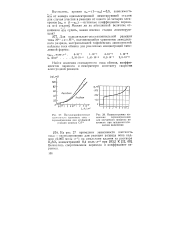 |
Осциллограмма изменения перенапряжения для изучаемого процесса во времени при гальваностатическом включении. [5] |
Можно ли по абсолютной величине отношения a / a судить, какая именно стадия лимитирующая. [6]
Этот коэффициент равен абсолютной величине отношения средней скорости, приобретаемой электронами проводимости в кристалле в направлении электрического поля к напряженности последнего. [7]
Эта граница определяется абсолютной величиной отношения числа, стоящего в правой части неравенства (3.1), к коэффициенту, стоящему при х2 в соответствующем неравенстве. Уравнение х6 21 не ограничивает рост переменной, так как данная переменная х2 в него не входит. Такой же знак будем использовать, когда свободный член и коэффициент при переменной в уравнении имеют одинаковые знаки, так как в этом случае нет ограничений на рост переменной. [8]
Коэффициент Пуассона ft - - абсолютная величина отношения поперечного укорочения к относительному продольному удлинению при простом растяжении прямого стержня. Коэффициент Пуассона имеет большое значение при расчетах на прочность и характеризует поперечную деформацию при продольном действии сил. [9]
Коэфициент Пуассона ц, - абсолютная величина отношения поперечного укорочения к продольному удлинению при простом растяжении прямого стержня в пределах применимости закона Гука. [10]
Основная статическая приведенная погрешность - абсолютная величина отношения наибольшей разности действительного и приведенного ходов к величине условного хода при незаполненном регулирующем органе и сальнике, затянутом усилием, обеспечивающим герметичность штока в рабочих условиях, выраженная в процентах. [11]
Основная статическая приведенная погрешность - абсолютная величина отношения наибольшей разности действительного и приведенного ходов к величине условного хода при незаполненном регулирующем органе и сальнике, затянутом усилием, обеспечивающим герметичность штока в рабочих условиях, выраженная в процентах. [12]
Основная приведенная погрешность б характеризуется абсолютной величиной отношения наибольшей разности действительного и приведенного ходов к величине условного хода при незаполненном регулирующем органе в сальнике, затянутом усилием, обеспечивающим герметичность штока в рабочих условиях. [13]
Коэффициент Пуассона v, определяемый как абсолютная величина отношения поперечной деформации и продольной деформации, которые обусловлены продольными нормальными напряжениями, принимает значения, изменяющиеся от близких к нулю-для некоторых пористых материалов до примерно равных одной второй ( это значение соответствует нулевому - изменению объема) для резины или для эквивалентной модели материала, проявляющей свойства пластического течения. Для большинства материалов, используемых в инженерной драктйке этот коэффициент имеет значение, близкое к 0 3, это же значение, за исключением специально оговоренных случаев, используется и в данной книге, когда формулы, содержащие коэффициент Пуассона v, сводятся к приближенным числовым значениям. [14]
Действительно, свойство П2 обеспечивает сохранение абсолютной величины отношения, а из свойства П1 следует, что его знак также остается прежним. [15]
Страницы: 1 2