Разрыв - кривая
Cтраница 4
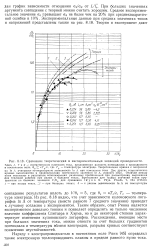
Из рис. 8.18 видно, что учет зависимости кулоновского логарифма In Л от температуры ( вместо равного 7 среднего значения) приводит к лучшему согласию с экспериментом. Таким образом, опыт Ринна является экспериментом довольно тонким и позволяет определить не только численное значение коэффициента Спитцера и Хэрма, но и до некоторой степени характеризует изменения кулоновского логарифма. Расхождения, имеющие место при больших значениях тока, можно отнести за счет больших градиентов потенциала и температуры вблизи электродов, разрывы кривых соответствуют появлению неустойчивостей. [47]
Уотермен [19] измерял сопротивление пластинчатых кристаллов MoS2 при температурах от 25 до 315 С. Он ашел, что при температуре ниже 310 С их электрическое сопротивление зависит от температуры. Он не сумел заметить каких-либо изменений кристаллической или химической структуры MoS2, но тем не менее зафиксировал явный разрыв кривой сопротивление - напряжение при 310 С. По мнению Уотермена, разрыв кривой происходит благодаря освобождению электронов при этой температуре. [48]
Площади, ограниченные осью ср и кривой ускорений выше оси р и ниже ее равны между собой. Иногда максимальный ход / zmax удерживается постоянным IB течение некоторого времени. Получаемая при этом форма кулачка создает дальнейший разрыв кривой ускорений, и поэтому она применяется только в механизмах, имеющих небольшое число оборотов. [49]
Было установлено, что в результате пульсирующего движения формируется динамическая атмосфера, протяженность которой на момент наинизшего положения поршня в 20 раз больше, чем в случае статической атмосферы, т.е. HCf 20 / У0 - На протяжении каждого периода формируется две ударные волны - при движении поршня вверх и его перемещении вниз. Как видно, несмотря на встречный поток ударная волна все же существенно ускоряется. На некоторой высоте, где благодаря прозрачности вещества движение становится изотермическим, фронт ударной волны движется с постоянной скоростью. В полном соответствии с наблюдениями получаются и разрывы кривой лучевых скоростей, хотя сброс вещества в межзвездное пространство в этом расчете не возникает. [50]
Если вместо такого свойства, как формы соединений, образуемых элементами, отложим другие свойства элементов, например удельный вес, температуру кипения соответствующих хлористых соединений, упругость растяжения и тому подобные физические свойства, то будем иметь волнообразные кривые. Если взять химические свойства, например кислотность и основность, или способность образовывать двойные соли, которая иногда может быть измеряема, а иногда примерно ощущаема, то мы всегда будем также иметь волнообразные кривые. Следовательно, всякие свойства состоят в периодической зависимости. При этом окажется, что происходит разрыв кривой в том месте, где находятся самые легкоплавкие тела: фтор и натрий, хлор и калий. Элементы, находящиеся около середины этих малых периодов, окажутся самыми тугоплавкими из всех тех, которые встречаются, например углерод, кремний и тому подобные простые тела. [51]
Страницы: 1 2 3 4