Малый разрыв

Cтраница 2

Характер аварийной остановки печи при прогарах труб змеевика определяется размерами и участками этих прогаров. Малый разрыв на отдулине или начинающийся прогар сопровождается незначительной течью сырья, наблюдаемой через гляделки или форсуночные амбразуры печи. В данном случае печь останавливают по нормальной схеме, а змеевик продувают. Вид продувки зависит от того, на каком участке змеевика находится прогоревшая труба: если ближе к выходу чз печи, продувку ведут против хода сырья, если же ближе к входу в печь - по ходу сырья. [16]

Порядок аварийной остановки печи при прогарах труб змеевика зависит от размеров и участков этих прогаров. Малый разрыв на отдулине или начинающийся прогар сопровождается незначительной течью сырья, наблюдаемой через гляделки или форсуночные амбразуры печи. [17]

Разрыв контактов не должен быть мал, так как в этом случае может иметь место перекрытие контактов электродугой при разрыве цепи. При малом разрыве контактов они подлежат замене. [18]

Необходимо иметь в виду, что поворот консоли 3 вместе с кабелем 5 при малых разрывах между точками А - Б вызовет сильное скручивание или схлестывание гибких проводов разных фаз. Поэтому использование поворотной консоли при малых разрывах между точками А и Б возможно только для изолированных кабелей на участке между точками А и В. [19]

Точные решения показали, что удельная теплоемкость должна иметь заметный разрыв непрерывности в точке перехода, хотя теплосодержание меняется непрерывно, так что процесс не связан с выделением скрытой теплоты. В противоположность этому все приближенные методы указывают на бесконечно малый разрыв непрерывности удельной теплоемкости. Еще неясно, будут ли кривые теплоемкости иметь такую же форму для трехмерной решетки, теория процессов упорядочения для которой еще не разработана. [20]

Пожары в городах и населенных пунктах, возникают при нарушении правил противопожарной безопасности, из-за неисправности электропроводки, распространения огня при лесных, торфяных и степных пожарах, при замыкании электропроводки во время землетрясений. Очень пожароопасны населенные пункты из деревянных построек с малыми разрывами между зданиями. При пожаре в населенных пунктах сильный ветер может разносить воспламененный материал и искры на значительные расстояния и этим распространять пожар. Пожары в городах и населенных пунктах оказывают морально-психологическое воздействие на людей и нарушают нормальную жизнедеятельность. [21]

Пожары в городах и населенных пунктах возникают при нарушении правил противопожарной безопасности, из-за неисправности электропроводки, распространения огня при лесных, торфяных и: тепных пожарах, при замыкании электропроводки во время землетрясений. Очень пожароопасны населенные пункты из деревянных построек с малыми разрывами между зданиями. При пожаре в населенных пунктах сильный ветер может разносить воспламененный материал и искры на значительные расстояния и этим распространять пожар. Пожары в городах и населенных пунктах оказывают морально-психологическое воздействие на людей и нарушают нормальную жизнедеятельность. [22]

Допустим, что некоторое случайное возмущение вызвало изменение профиля т ( а) от рис. 3.4, а к рис. 3.4 6; мы хотим знать, оставит ли этот малый разрыв прежним значение скачка на - фронте главной волны, догнав ее или отстав, или уменьшит его на постоянную величину. [23]

Представим себе тело разрезанным на малые параллелепипеды. Если каждый из этих параллелепипедов получит произвольные деформации, то из отдельных деформированных параллелепипедов не удастся вновь сложить непрерывное твердое тело: в некоторых точках окажутся после деформации бесконечно малые разрывы. Уравнения (2.10) и дают такие зависимости между составляющими деформации, при выполнении которых тело после деформации получается сплошным, или непрерывным. [24]

Представим себе тело разрезанным на малые параллелепипеды. Если каждый из этих параллелепипедов получит произвольные деформации, то из отдельных деформированных параллелепипедов не удастся вновь сложить непрерывное твердое тело: в некоторых точках после деформирования возникнут бесконечно малые разрывы. Уравнения же (2.8) устанавливают такие зависимости между составляющими деформации, при удовлетворении которых тело и после деформирования остается сплошным, или непрерывным. [25]

Необходимость существования этих зависимостей мы обосновали аналитическим путем, сопоставляя число функций (2.2) с числом функций (2.12) и принимая во внимание зависимости между ними (2.6); той же цели можно достичь геометрическим путем. Для этого представим себе упругое тело разрезанным на малые параллелепипеды и дадим каждому из них деформацию, определяемую шестью величинами (2.12); легко сообразим, что если составляющие деформации (2.12) не связаны между собою определенными зависимостями, то из отдельных деформированных параллелепипедов не удастся вновь сложить непрерывное ( деформированное) твердое тело. Уравнения (2.15) и доставляют нам эти зависимости; если мы при задании деформаций (2.12) не примем их во внимание, то после деформации тела во всех точках его окажутся бесконечно малые разрывы. Эти соображения придают новый смысл уравнениям (2.15), и с этой новой точки зрения уравнения (2.15) называются уравнениями неразрывности или совместности деформаций. Выведены они Сен-Венаном и часто, называются уравнениями Сен-Венана. [26]

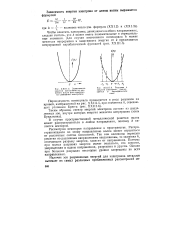Зависимость энергии электронов от волнового числа для совершенно свободных электронов. [27]

Рассмотрим некоторое направление в пространстве. Распространяющаяся по этому направлению волна может отразиться от различных систем плоскостей. Так как величины периодов решетки по различным направлениям неодинаковы, то значения k, отвечающие разрыву энергии, зависят от направления. Поэтому при малых разрывах энергии может оказаться, что энергия, запрещенная в одном направлении, разрешена в другом. Однако при больших разрывах некоторые уровни запрещены во всех направлениях. [28]

Страницы: 1 2