Апериодический разряд

Cтраница 1

Апериодический разряд конденсатора-разряд, при котором не происходит затухающих коле-баеий напряжения на обкладках конденсатора, а это напряжение постепенно убывает до нуля. [1]

Для апериодического разряда формула ( 2 - 23) теряет смысл. [2]

При апериодическом разряде напряжение на конденсаторе и ток уменьшаются до нуля при t оо. [3]

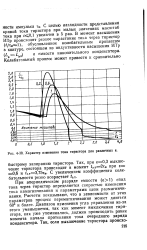Характер изменения тока тиристора для различных е. [4]

При апериодическом разряде емкости ( е1) спад тока через тиристор определяется скоростью изменения тока намагничивания и параметрами цепи размагничивания. Расчеты показывают, что в зависимости от этих параметров процесс перемагничивания может длитмгя 60 и более. Диапазон изменения угла управления из-за этого уменьшается, так как момент выключения тиристора, как уже упоминалось, должен происходить ранее момента начала протекания тока очередного заряда конденсатора. [5]

Такой односторонний разряд конденсатора называют апериодическим разрядом. [6]

Включение в контур сопротивления позволяет получить апериодический разряд ( CRL) с регулируемой амплитудой тока. [7]

С колебания отсутствуют; происходит так называемый апериодический разряд, т.е. постепенная ( без колебаний) разрядка конденсатора через катушку. [8]

При каких соотношениях между параметрами контура происходит апериодический разряд. [9]

Задача III.4. Доказать, что в случае апериодического разряда индуктивное напряжение всегда меньше емкостного, кривые UL и ис не могут пересечься. [10]

Данный случай при 5 оз0 является предельным случаем апериодического разряда, так как при дальнейшем уменьшении г ниже значения 2 - JIJC разряд становится колебательным. [11]

Данный случай при 8 со0 является предельным случаем апериодического разряда, так как при дальнейшем уменьшении т ниже значения 2 У L / C разряд становится колебательным. [12]

Строят график U ( /) - кривую апериодического разряда. [13]

Данный случай при б ю0 является предельным случаем апериодического разряда, так как при дальнейшем уменьшении г ниже значения 2 Y L / C разряд становится колебательным. [14]

Данный случай при б ( о является предельным случаем апериодического разряда, так как при дальнейшем уменьшении г ниже значения 2 1 / - разряд становится колебательным. Пусть корни характеристического уравнения являются комплексными. [15]

Страницы: 1 2 3 4