Младший разряд - произведение
Cтраница 1
Младшие разряды произведения нужны также и для того, чтобы сохранить точность после нормализации и округления. При последующих сдвигах код со старшей ячейки переходит на соседние разряды, а его место занимают коды, поступающие с сумматора. [1]
Вывод младших разрядов произведения значительно облегчает выполнение действий с удвоенным числом разрядов. Вычитание модулей используется в основном для определения точности результатов, сложение и вычитание порядков равносильно умножению на 2 ( п - целое число, которое может быть как положительным, так и отрицательным), но выполняется значительно быстрее умножения. [2]
Вывод младших разрядов произведения значительно облегчает выполнение действий с удвоенным ( или большим) числом разрядов. [3]
Если 9 младших разрядов произведения равны нулю, то устанавливается в 1 индикатор НУЛЬ. Если 9 старших разрядов произведения не равны нулю, то устанавливается в 1 указатель ПЕРЕПОЛНЕНИЕ. Возможны случаи установки в 1 одновременно индикатора НУЛЬ и указателя ПЕРЕПОЛНЕНИЕ. Режим округления для оператора УЦДР не используется. [4]
Во время сдвига младшего разряда произведения в регистр MR метка М2 из 11-го разряда регистра АСО в обычной последовательности перезаписывается в тетраду А. Во время цикла записи цифра из тетрады триггеров Е перезаписывается в 11 - й разряд регистра АСО. [5]
Результатом являются тридцать шесть младших разрядов произведения ( девять десятичных цифр) и знак произведения. Если хотя бы один из старших разрядов произведения отличен от нуля, то устанавливается в единицу указатель ПЕРЕП. Таким образом, одновременно могут устанавливаться в единицу индикатор НУЛЬ и указатель ПЕРЕП. Режим округления не влияет на результат операции. [6]
Для этого производится отсечение ненужных младших разрядов произведения, причем последний отсекаемый разряд округляется. Это значит, что если содержимое этого разряда равно пяти или больше пяти, то оно преобразуется в единицу переноса в старший разряд, если же меньше пяти, то единица переноса не образуется. [7]
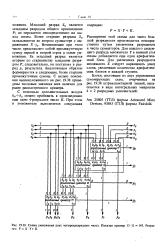 |
Схема умножения двух четырехразрядных чисел. Показан пример 13 - 11 143. Результат. P X-Y K. [8] |
Младший разряд S0 является младшим разрядом общего произведения Р; он передается непосредственно на выход схемы. Более старшие разряды S0 складываются во втором сумматоре с выражением Х - уг. Возникающее при этом число представляет собой промежуточную сумму первой и второй строк в схеме умножения. Ее младший разряд является вторым по старшинству младшим разрядом Р; следовательно, он поступает в разряд pl результата. Аналогичным образом формируются и следующие, более старшие промежуточные суммы. С целью пояснения вышеизложенного на рис. 19.38 приведены числовые значения всех величин для ранее рассмотренного примера. [9]
Результатом оператора являются тридцать шесть младших разрядов произведения со знаком произведения. Результат в МОЗУ не записывается. Старшие разряды произведения не сохраняются. Если хотя бы один из отбрасываемых разрядов не нуль, устанавливается в единицу указатель ПЕРЕП. [10]
В результате сдвигов будут потеряны п младших разрядов произведений. Для округления произведения отводится дополнительный разряд, в котором сохраняется последний из сдвигаемых разрядов результата для прибавления к нему единицы. [11]
Регистр Т одновременно используется для хранения младших разрядов произведения, не участвующих в последующих операциях суммирования частичных произведений. Выдвигаемый из регистра младший разряд множителя принимается в триггер Z БМУ, и по содержимому этого триггера осуществляется разветвление процесса: при Z 1 к содержимому регистра R2 прибавляется множимое, при Z 0 акт суммирования пропускается. Возникающий в процессе суммирования перенос помещается в триггер С регистра признаков БМУ. [12]
В итоге в регистре 1 получается п младших разрядов произведения, а в сумматоре - п старших разрядов произведения. Сумматор должен иметь п 1 разрядов. [13]
В машинах типа М-20 существует операция выдачи младших разрядов произведения ( х б; 47), позволяющая получить младшие разряды мантиссы произведения. [14]
Операции над числами ( за исключением выдачи младших разрядов произведения, сложения и вычитания порядков) имеют модификации, состоящие в выдаче результатов с нормализацией или без нее и с округлением или без округления. РОП) находится единица, то нормализация сдвигом влево не производится. [15]
Страницы: 1 2 3 4