Операторная величина
Cтраница 1
Операторные величины следует обозначать по типу: 1 ( р) или I ( s) - операторный ток. [1]
Прямой шрифт соответствует операторным величинам: светлый - скалярам, а полужирный - векторам. [2]
Комплексы Xd ( jh), Xq ( jh), G ( jh) получаются из операторных величин Xd ( p), Xq ( p), G ( p) заменой р на jh, где h - относительная частота колебаний. [3]
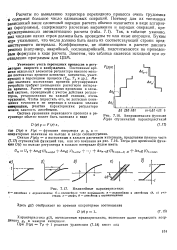 |
Аппроксимация функции F ( p x ступенчатой характеристикой.| Нелинейные характеристики. [4] |
Где Dip) и F ( p) - функции оператора р; у, х - - операторные величины на выходе и входе соответственно. [5]
Отметим, что и в более общем случае, когда Ец, Е &, л21 и Gn есть операторные величины, можно с помощью аппроксимации (15.9) получить соответствующие аппроксимирующие выражения. [6]
Здесь в отличие от схемы на рис. 7 - 2 учтена емкость коллекторного перехода С, а коэффициент передачи р считается операторной величиной. Поскольку параметры С и г являются функциями Р, они тоже являются операторными величинами, что отражено точками над их обозначениями. Как обычно, при импульсном анализе мы будем пользоваться оператором s, а при гармоническом - оператором / со. [7]
 |
Принципиальная ( а и эквивалентная ( б схемы каскада с коллекторным фильтром для коррекции искажений вершины импульса. [8] |
Здесь в отличие от схемы на рис. 7 - 2 учтена емкость коллекторного перехода С, а коэффициент передачи 3 считается операторной величиной. Поскольку параметры С и r являются функциями р они тоже являются операторными величинами, что отражено точками над их обозначениями. Как обычно, при импульсном анализе мы будем пользоваться оператором s, а при гармоническом - оператором / со. [9]
Здесь в отличие от схемы на рис. 7 - 2 учтена емкость коллекторного перехода С, а коэффициент передачи 3 считается операторной величиной. Поскольку параметры С и r являются функциями р они тоже являются операторными величинами, что отражено точками над их обозначениями. Как обычно, при импульсном анализе мы будем пользоваться оператором s, а при гармоническом - оператором / со. [10]
Здесь в отличие от схемы на рис. 7 - 2 учтена емкость коллекторного перехода С, а коэффициент передачи р считается операторной величиной. Поскольку параметры С и г являются функциями Р, они тоже являются операторными величинами, что отражено точками над их обозначениями. Как обычно, при импульсном анализе мы будем пользоваться оператором s, а при гармоническом - оператором / со. [11]
Последние уравнения состояния, в отличие от уравнений Максвелла, определены только при распространении волн перпендикулярно ориентации волокон. Из изложенного следует, что аналогии могут наблюдаться только в стационарных полях. Входящие в операторы новые эффективные параметры, такие как модули упругости, коэффициенты теплопроводности, коэффициенты диэлектрической проницаемости и другие, являются постоянными, найденными эмпирически. В действительности, в случае, когда матрица композита полимерная, последние, как и многие другие материалы, способны при длительной постоянной нагрузке или при переменных нагрузках проявлять неупругие свойства и поэтому являются операторными величинами. Аналогичными свойствами обладают диэлектрические и другие проницаемости при высоких частотах изменения электромагнитного поля. Для умеренной интенсивности полей указанные операторы могут быть построены в линейном приближении. Пользуясь принципом Вольтерра и заменяя в формулах физические постоянные соответствующими линейными операторами, удается расширить область применимости уравнений состояния. [12]
Страницы: 1