Ранг

Cтраница 3

Ранг этой матрицы равен двум, следовательно, один из написанных маршрутов не является независимым. Это видно и из применения правила Гориути, так как в данном случае имеем одно независимое промежуточное соединение ( Спов равнозначно свободному месту поверхности угля) при трех стадиях. Любая пара маршрутов здесь образует базис, полностью описывающий все превращение в данной системе из 3 - х стадий и одного независимого промежуточного соединения СОПОВ. [31]

Ранг - это количественная условная оценка параметра оптимизации, разделяющая разные качества или ограничивающая область качества. [32]

Ранг всякой матрицы совпадает с наивысшим порядком ее отличных от нуля миноров. [33]

Ранг этой матрицы равен двум: минор второго порядка, стоящий в левом верхнем углу, отличен от нуля, но оба минора третьего порядка, его окаймляющие, равны нулю. Отсюда следует, что векторы at, a, составляют в заданной системе одну из максимальных линейно независимых подсистем. [34]

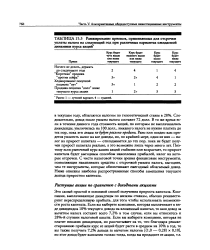Ранжирование приемов, применяемых для отсрочки уплаты налога на следующий год при различных вариантах ожидаемой динамики курса акций. [35]

Ранги: 1 - лучший вариант, 4 - худший. [36]

Ранг указывает то место, которое занимает данная единица совокупности среди других единиц. [37]

Ранг и сигнатура квадратичной формы ( 4) не меняются при изменении декартовой системы координат. [38]

Ранг и сигнатура квадратичной формы ( 5) не меняются при замене декартовой системы координат. [39]

Ранг этой системы равен также п - k, поскольку строки матрицы перехода линейно независимы. [40]

Ранг и сигнатура малой квадратичной формы ( 4) не меняются при изменении декартовой системы координат. [41]

Ранг и сигнатура большой квадратичной формы ( 5) не меняются при замене декартовой системы координат. [42]

Ранг этой матрицы не меньше чем я-г, так как в ней есть я-г линейно независимых столбцов. [43]

Ранг этой системы равен также п - k, поскольку строки матрицы перехода линейно независимы. [44]

Ранг и сигнатура малой квадратичной формы ( 4) не меняются при изменении декартовой системы координат. [45]

Страницы: 1 2 3 4