Экспоненциальный распад

Cтраница 1

Экспоненциальный распад приводит к лоренцевской форме спектральной линии. Отсюда, в частности, следует, что у спектра не существует второго момента. В реальных физических системах должен существовать некоторый механизм, обрезающий крыло лоренциана. [1]

Хорошо известно, что можно исследовать те вклады в лоренцевскую форму линии, которые возникают на различных участках экспоненциального распада ядерного состояния. Начальный этап распада делает линию шире естественной, более поздние этапы - более узкой. Введение зависящего от времени фактора f уменьшает вклад от начального этапа распада и, таким образом, позволяет получить более узкую линию. Но этот эффект до сих пор не был обнаружен. [2]

Например, с помощью этого соотношения можно описать различные типы поведения популяций: экспоненциальный рост, стационарное состояние, экспоненциальный распад и т.п. В соотношении ( 25) параметр р описывает связь между двумя системами ql и 72, и если сила связи регулируется извне, то р играет роль управляющего параметра. [3]

Например, с помощью этого соотношения можно описать различные типы поведения популяции: экспоненциальный рост, стационарное состояние, экспоненциальный распад и т.п. В соотношении (2.7) параметр Р описывает связь между двумя системами qi и q2 и, если сила связи регулируется извне, то ( 3 играет роль управляющего параметра. [4]

В такой теории на ранней стадии горячей Вселенной, вблизи сингулярности, кварков много, но они полностью вымирают за счет экспоненциального распада к настоящему времени. [5]

Таким образом, когда молекула N20 термически активирована до энергии, превышающей низший диссоциационный предел, она имеет гораздо большее время жизни, чем ожидается на основании случая II предиссоциации. Из-за большого времени жизни экспоненциальный распад наблюдается при гораздо более низких давлениях, чем в других случаях. Сходная ситуация: возникла бы в молекуле С02, но ее термический распад требует гораздо более высоких температур и еще не изучался. [6]

Рассмотрим сначала случай fci2 2 А / 23 - В этом случае третий процесс ( с масштабом характерных времен Ti2 fc 1) гораздо быстрее, чем второй. В течение весьма непродолжительного времени ( экспоненциальный распад согласно (7.29)) концентрация [ S ] i компонента S становится почти нулевой. Это значит, что частицы компонента Si очень быстро реагируют с частицами компонента S. [7]

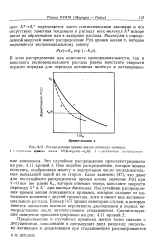Распределения времен жизни активных молекул. - случайные времена жизни [ P ( T feaexp ( - . ат ]. 2 - неслучайное рэгпрецэлениэ. [8]

Оно подобно распределению, которое можно получить, подбрасывая монету и подсчитывая число последовательных выпаданий одной из ее сторон. Было замечено [47], что даже для неслучайного распределения времен жизни значение Р ( т) при т0 все же равно ka, которое отвечает теперь константе скорости перехода А в А при высоких давлениях. Неслучайные распределения времен жизни описываются кривыми, которые спадают от начального значения с другой скоростью, хотя и имеют вид экспоненциального распада. Банкер [47] привел некоторые случаи, в которых имеется аномально высокая вероятность диссоциации в период непосредственно после активирующего столкновения. [9]

Если период полураспада лежит в пределах от нескольких секунд до нескольких лет, то его значение обычно определяется в результате ряда последовательных измерейий активности, производимых с помощью соответствующего прибора через удобные промежутки времени. По оси абсцисс откладывается время измерения, а по оси ординат - соответствующие значения IgA. Из полученного графика определяется период полураспада. Желательно наблюдать чистый экспоненциальный распад в течение времени, равного нескольким периодам полураспада. [10]

Случай II предиссоциации основных электронных состояний хорошо известен как химическая реакция мономолекулярного распада. Такой распад наблюдается, когда данный молекулярный газ нагревается до достаточно высокой температуры. Если время жизни больше, чем время между последовательными столкновениями, перед распадом может происходить дезактивация. В результате имеется экспоненциальный распад, как при радиоактивном распаде, причем постоянная распада ( константа скорости) пропорциональна вероятности у перехода без излучения. Известно несколько процессов этого типа ( Слейтер [36], Раис [1070]), и они должны быть окончательно отнесены к случаю II предиссоциации, хотя подобная интерпретация даже в литературе на эту тему обычно не дается. При низких давлениях скорость реакции определяется скоростью активации, так как каждая молекула распадается сразу после активации. Поэтому в области низкого давления реакция распада является реакцией второго порядка. [11]

И для самого лазера, и для многих спектроскопических систем оба оптически активных уровня, связанные излучением, спонтанно распадаются в более низкие состояния. Частицы фактически исчезают из области взаимодействия, если распад происходит на ненаблюдаемые уровни. Поэтому скорость распада определяет время взаимодействия с полем. Аналогичными ограничивающими время взаимодействия процессами являются тушащие столкновения, уход атомов на стенки или химические реакции. Наиболее часто именно эти случайные процессы, описываемые экспоненциальным распадом, ограничивают время воздействия излучения в лазерной спектроскопии атомов. Только основное состояние и некоторые мета-стабильные уровни живут достаточно долго, так что время стационарности определяется другими процессами. [12]

В приложениях, где требуется очень сильное поле, часто необходимы импульсные лазеры. В этом случае время воздействия определяется временной зависимостью амплитуды поля. Аналогичными являются времяпролетные ограничения стационарности. Они проявляются, например, в тех случаях, когда долго-живущая частица ( особенно молекула), не распадаясь, пролетает через лазерный пучок. Если непрерывный лазер имеет поперечную структуру излучения, пролетные частицы оказываются в поле переменной во времени амплитуды. Распределение времен взаимодействия зависит, в частности, и от распределения частиц по скоростям. Это в свою очередь зависит от того, как, в кювете или в пучке, проводится измерение. В молекулярной спектроскопии время пролета через область поля часто является ограничивающим параметром. Конечно, в этом случае экспоненциальный распад не является адекватным описанием в уравнениях Для матрицы плотности. [13]

Страницы: 1